
3.某小组有8名同学,从中选出2名男生、1名女生,分别参加数理化单科竞赛,每人参加一种共有90种不同的参赛方案,则男女生的个数应是( )
(A)男6女2 (B)男5女3
(C)男3女5 (D)男2女6
2.设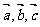 是非零向量,下列命题正确的是 ( )
是非零向量,下列命题正确的是 ( )
A.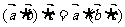
B.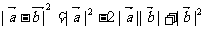
C.若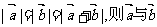 的夹角为60°
的夹角为60°
D.若 的夹角为60°
的夹角为60°
1.已知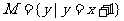 、
、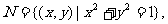 则集合
则集合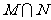 中元素的个数是 A.0 B.1 C.2 D.多个
中元素的个数是 A.0 B.1 C.2 D.多个
22.
(12分)已知函数
(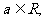
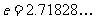 ) 且
) 且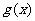 在x=1处取得极值.
在x=1处取得极值.
(1)求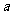 的值和
的值和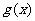 的极小值;
的极小值;
(2) 判断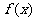 在其定义域上的单调性, 并予以证明;
在其定义域上的单调性, 并予以证明;
(3)已知△ ABC的三个顶点A、B、C都在函数y=f (x)的图象上,且横坐标依次
成等差数列,求证:△ABC是钝角三角形, 但不可能是等腰三角形.
21. (12分)设平面上的动向量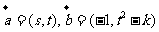 ,其中
,其中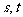 为不同时为0的两个实数,实数
为不同时为0的两个实数,实数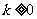 ,满足
,满足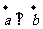
(1) 求函数关系式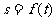
(2) 若函数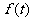 在
在 上单调递增,求
上单调递增,求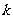 的范围;
的范围;
(3) 对上述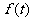 ,当
,当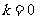 时,存在正项数列
时,存在正项数列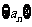 满足
满足 ,其中
,其中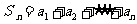 ,证明:
,证明: 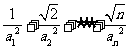 <3
<3
20.(12分)已知函数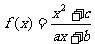 为奇函数,
为奇函数,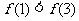 ,且不等式
,且不等式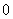 ≤
≤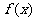 ≤
≤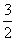 的解集是
的解集是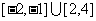 .
.
(Ⅰ)求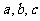 ;
;
(Ⅱ)是否存在实数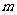 使不等式
使不等式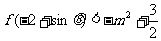 对一切
对一切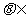 R成立?若成立,求出
R成立?若成立,求出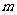 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.
19.(12分)数列{an}中,a1=8,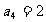 ,且满足:
,且满足: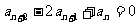 (n∈N*),
(n∈N*),
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设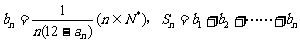 ,是否存在最大的整数m,使得任意的n均有
,是否存在最大的整数m,使得任意的n均有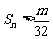 总成立?若存在,求出m若不存在,请说明理由.
总成立?若存在,求出m若不存在,请说明理由.
17(13分)若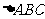 中,a,b,c分别是
中,a,b,c分别是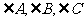 的对边,且
的对边,且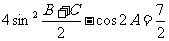 ,
,
(1) 求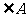 ;
;
(2) 若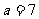 ,
,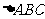 的面积为
的面积为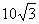 ,求b+c的值。
,求b+c的值。
18. (13分)美国蓝球职业联赛(NBA)某赛季的总决赛在湖人队与活塞队之间进行, 比赛采取七局四胜制, 即若有一队胜四场,则此队获胜且比赛结束. 因两队实力非常接近,在每场比赛中每队获胜是等可能的.据资料统计, 每场比赛组织者可获门票收入100万美元. 求在这次总决赛过程中,比赛组织者获得门票收入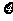 (万美元)的概率分布及数学期望
(万美元)的概率分布及数学期望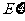 .
.
16.给出下列4个命题:
①函数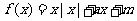 是奇函数的充要条件是m=0:
是奇函数的充要条件是m=0:
②若函数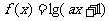 的定义域是
的定义域是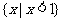 ,则
,则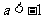 ;
;
③若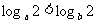 ,则
,则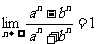 (其中
(其中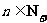 );
);
④圆: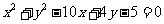 上任意点M关于直线
上任意点M关于直线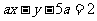 的对称点,
的对称点,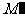 也在该圆上.填上所有正确命题的序号是________.
也在该圆上.填上所有正确命题的序号是________.
15.定义:若存在常数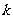 ,使得对定义域
,使得对定义域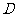 内的任意两个
内的任意两个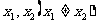 ,均有
,均有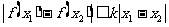 成立,则称函数
成立,则称函数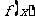 在定义域
在定义域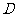 上满足利普希茨条件。若函数
上满足利普希茨条件。若函数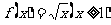 满足利普希茨条件,则常数
满足利普希茨条件,则常数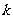 的最小值为 。
的最小值为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com