
8. 已知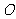 为原点,点
为原点,点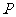 (x,y)在单位圆x2+y2=1上,点
(x,y)在单位圆x2+y2=1上,点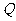 (2cos
(2cos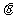 ,2sin
,2sin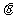 )且
)且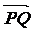 =(
=(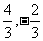 ),则
),则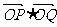 的值为( )
的值为( )
A.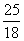 B.
B.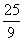 C.2 D.
C.2 D.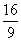
7.某地区对用户用电推出两种收费办法,供用户选择使用:一是按固定电价收取;二是按分时电价收取,即在固定电价的基础上,平时时段电价每千瓦时上浮0.03元;低谷时段电价每千瓦时下浮0.25元.若一用户某月平时时段用电140千瓦时,低谷时段用电60千瓦时,则相对于固定电价收费该月该用户
A.多付电费10.8元 B.少付电费10.8元 C.少付电费15元 D.多付电费4.2元
6.已知椭圆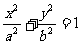 (a>b>0)的左焦点是F,A、B分别是左顶点和上顶点 ,若F到直线AB的距离是
(a>b>0)的左焦点是F,A、B分别是左顶点和上顶点 ,若F到直线AB的距离是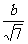 ,则椭圆的离心率是( )
,则椭圆的离心率是( )
A.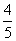 B.
B.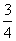 C.
C.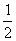 D.
D.
5. 已知xy=14,0<x<y<1,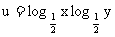 ,则
,则
A.u≤1 B.u<1 C.u>1 D.u≥1
4. 不等式f(-x)=ax2-x-c>0的解集为{x|-2<x<1},则函数y=f(x)的图象为
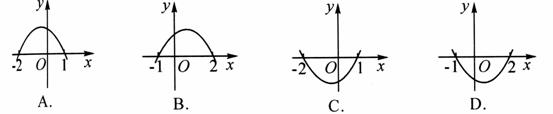
3.在 ABC中,若cosAcosB>sinAsinB,则方程x2cosA+y2cosC=1表示
ABC中,若cosAcosB>sinAsinB,则方程x2cosA+y2cosC=1表示
A 焦点在x轴上的椭圆 B焦点在y轴上的椭圆
C 焦点在x轴上的双曲线 D焦点在y轴上的双曲线
2.在等差数列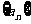 中,若
中,若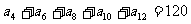 ,则
,则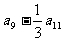 的值为( )
的值为( )
A.14 B.15 C.16 D.17
1.已知集合 ,那么
,那么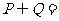 ( )
( )
A.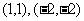 B.
B.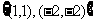 C.
C.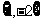 D.
D.
22.(本小题满分14分)已知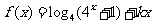
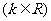 是偶函数.
是偶函数.
(1) 求k的值;
(2)
证明:对任意实数b,函数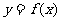 的图象与直线
的图象与直线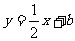 最多只有一个交点;
最多只有一个交点;
设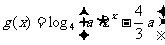 ,若函数
,若函数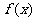 与
与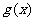 的图象有且只有一个公共点,求实数a的取值范围.
的图象有且只有一个公共点,求实数a的取值范围.
21.(本小题满分12分)设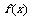 是定义在
是定义在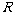 上的奇函数,且函数
上的奇函数,且函数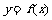 与
与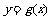 的图象关于直线
的图象关于直线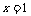 对称,当
对称,当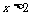 时,
时,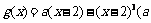 为常数)
为常数)
(1)求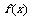 的解析式;
的解析式;
(2)若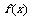 对区间
对区间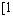 ,
, 上的每个
上的每个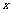 值,恒有
值,恒有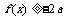 成立,求
成立,求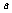 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com