
4.已知 ,则
,则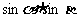 的最大值为( )
的最大值为( )
A.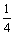 B.
B.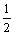 C.1 D.无最大值
C.1 D.无最大值
3.若一个直角三角形的三条边所在直线的斜率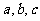 都存在,且
都存在,且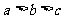 ,则方程
,则方程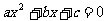 的根的情况是( )
的根的情况是( )
A.只有一个实数根 B.可能有一个根等于0
C.一定有两个不相等的实数根 D.可能没有实数根
2.若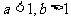 ,那么下列命题中正确的是( )
,那么下列命题中正确的是( )
A.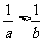 B.
B.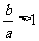 C.
C.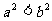 D.
D.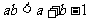
1.若集合A有2个元素,集合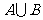 有4个元素,则集合B中元素的个数是( )
有4个元素,则集合B中元素的个数是( )
A.2 B.2或3 C.2或3或4 D.无法确定
(17)(本小题满分13分)已知向量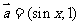 ,
,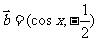 .
.
(Ⅰ)当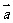 ⊥
⊥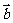 时,求|
时,求|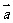 +
+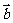 |的值;
|的值;
(Ⅱ)求函数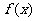 =
=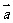 ·(
·(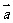 -
-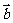 )的值域.
)的值域.
(18)(本小题满分13分)已知函数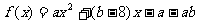 ,当
,当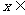 (
(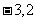 )时,
)时,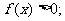 当
当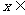 (
( )
)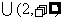 时,
时,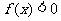
(Ⅰ)求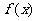 在[0,1]内的值域;
在[0,1]内的值域;
(Ⅱ)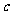 为何值时,
为何值时,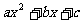 ≤0的解集为R.
≤0的解集为R.
(19)(本小题满分13分)设数列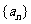 的前n项和为
的前n项和为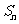 ,数列
,数列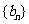 的前n项和为
的前n项和为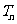 ,已知
,已知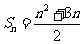 ,
,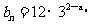 .
.
(Ⅰ)求数列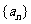 的通项公式;
的通项公式;
(Ⅱ)是否存在一个最小正整数M,当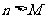 时,
时,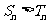 恒成立?若存在,求出这个M的值;若不存在,请说明理由.
恒成立?若存在,求出这个M的值;若不存在,请说明理由.
(20)(本小题满分13分)已知函数f(x)=
ax + 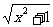 是R上的减函数,求a 的范围。
是R上的减函数,求a 的范围。
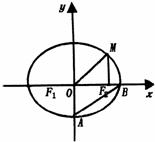
(21)(本小题满分12分)如图,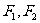 分别是椭圆
分别是椭圆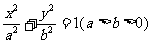 的左右焦点,M为椭圆上一点,
的左右焦点,M为椭圆上一点,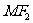 垂直于
垂直于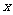 轴,且OM与椭圆长轴和短轴端点的连线AB平行,
轴,且OM与椭圆长轴和短轴端点的连线AB平行,
(Ⅰ)求椭圆的离心率;
(Ⅱ)若G为椭圆上不同于长轴端点任一点,求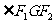 取值范围;
取值范围;
(Ⅲ)过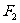 且与OM垂直的直线交椭圆于P,Q.若
且与OM垂直的直线交椭圆于P,Q.若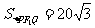 ,求椭圆的方程.
,求椭圆的方程.
(22)(本小题满分12分)已知函数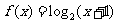 ,当点M(x,y)在
,当点M(x,y)在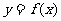 的图象上运动时,点N
的图象上运动时,点N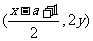 (
(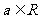 )在函数
)在函数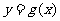 的图象上运动.
的图象上运动.
(Ⅰ)求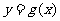 的解析式;
的解析式;
(Ⅱ)若函数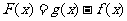 的最小值为4,求函数
的最小值为4,求函数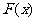 的单调区间;
的单调区间;
(11) 不等式4 x - 2 x +1 < 0 的解集是 。
(12)已知向量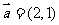 ,
,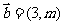 ,若
,若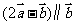 ,则m的值是 .
,则m的值是 .
(13)在条件 下,则
下,则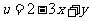 的最大值是
.
的最大值是
.
(14)设有两个命题:①关于x的不等式 的解集是R,②函数
的解集是R,②函数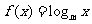 是减函数.如果这两个命题中有且只有一个真命题,则实数m的取值范围是
.
是减函数.如果这两个命题中有且只有一个真命题,则实数m的取值范围是
.
(15) 已知数列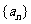 满足
满足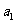 =24,且
=24,且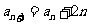 ,那么
,那么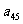 =
.
=
.
(16) .已知函数 f(x) =︱x – n –0.5︱,x∈[n, n+1 ),n是整数。 以下有四个命题
①f(x)是奇函数。 ②f(x)是偶函数。 ③f(x)是周期函数。④f(x) ≤0.5
其中正确命题的序号是____________。
(1)函数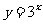 的反函数是
的反函数是
(A) 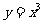 (B)
(B) 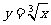 (C)
(C) 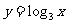 (D)
(D) 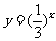
(2)将函数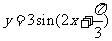 的图象按向量
的图象按向量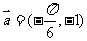 平移后所得图象的解析式是
平移后所得图象的解析式是
(A) 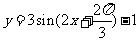 (B)
(B) 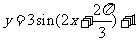
(C) 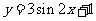 (D)
(D)
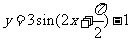
(3)在区间 上递增的函数是
上递增的函数是
(A)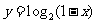 (B)
(B) 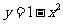 (C)
(C) 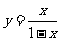 (D)
(D) 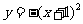
(4)函数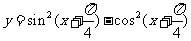 是
是
(A) 周期为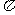 的奇函数 (B) 周期为
的奇函数 (B) 周期为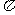 的偶函数
的偶函数
(C)
周期为2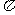 的奇函数
(D) 周期为2
的奇函数
(D) 周期为2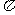 的偶函数
的偶函数
(5)已知集合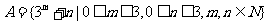 ,则集合A中元素个数为
,则集合A中元素个数为
(A) 16 (B)14 (C)9 (D)8
(6)条件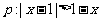 ,条件
,条件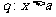 ,若p是q的充分不必要条件,则a的取值范围是
,若p是q的充分不必要条件,则a的取值范围是
(A) 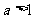 (B)
(B) 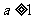 (C)
(C) 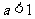 (D)
(D) 
(7)定义在R上的函数 f (x) 在x ≥1时,f (x) = log 2 x ,且 f(x +1) 是偶函数。则f (0)=
(A) 0 (B) 1 (C) -1 (D) 2
(8)已知过点P(-2,2)且垂直于向量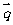 =(3,4)的直线与圆
=(3,4)的直线与圆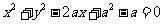 相切,则实数a的值为
相切,则实数a的值为
(A) 4 (B) 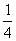 (C) 4或
(C) 4或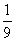 (D) -1或
(D) -1或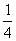
(9)已知曲线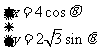 上一点P到点A(-2,0)、点B(2,0)的距离之差为2,则△PAB是
上一点P到点A(-2,0)、点B(2,0)的距离之差为2,则△PAB是
(A)锐角三角形 (B) 直角三角形 (C)钝角三角形 (D) 等腰三角形
(10)设数列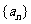 的前n项和为
的前n项和为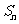 ,令
,令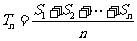 ,称
,称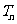 为数列
为数列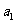 ,
,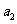 ,……,
,……,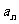 的“理想数”,已知数列
的“理想数”,已知数列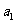 ,
,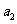 ,……,
,……, 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 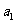 ,
,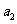 ,……,
,……, 的“理想数”为
的“理想数”为
(A) 2002 (B) 2004 (C) 2006 (D) 2008
22.(本题满分18分)(1)5分,(2)5分,(3)8分
定义:若存在常数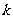 ,使得对定义域D内的任意两个不同的实数
,使得对定义域D内的任意两个不同的实数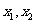 ,均有:
,均有: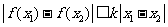 成立,则称
成立,则称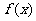 在D上满足利普希茨(Lipschitz)条件.
在D上满足利普希茨(Lipschitz)条件.
(1)试举出一个满足利普希茨(Lipschitz)条件的函数及常数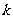 的值,并加以验证;
的值,并加以验证;
(2)若函数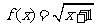 在
在 上满足利普希茨(Lipschitz)条件,求常数
上满足利普希茨(Lipschitz)条件,求常数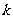 的最小值;
的最小值;
(3) 现有函数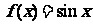 ,请找出所有的一次函数
,请找出所有的一次函数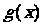 ,使得下列条件同时成立:
,使得下列条件同时成立:
①函数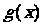 满足利普希茨(Lipschitz)条件;
满足利普希茨(Lipschitz)条件;
②方程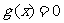 的根
的根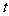 也是方程
也是方程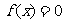 的根,且
的根,且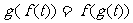 ;
;
③方程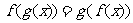 在区间
在区间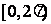 上有且仅有一解.
上有且仅有一解.
21.(本题满分16分)(1)5分,(2)5分,(3)6分)
据历史记载,美日在中途岛(Midway)海战前,美方截获了日方密码电报,据美方已破译的密码得知,日方将向某岛进行军事活动,但关键含有地点的部分却被日方换成了另一种密码.经专家研究,估计是一种密匙密码,且密匙为3位.所谓密匙密码是指:将一段英文字母的明文(未加密前原文)经过对某一组数字(即密匙)的变换,改变成了另一组英文字母成为密文(加密后的文字)例如:明文: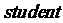 (不计空格,不计大小写)在密匙为:1 9 2 的条件下,变换过程如下图所示:
(不计空格,不计大小写)在密匙为:1 9 2 的条件下,变换过程如下图所示:
|
s |
t |
u |
d |
e |
n |
t |
|
1 |
9 |
2 |
1 |
9 |
2 |
1 |
|
t |
c |
w |
e |
n |
p |
u |
则密文为: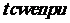 ,试根据上面信息回答下面问题:
,试根据上面信息回答下面问题:
(1)在密匙为111的条件下,填写下表,并写出密文;
|
s |
t |
u |
d |
e |
n |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
密文为____________________.
(2)若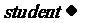
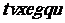 请填写下表,并写出密匙;
请填写下表,并写出密匙;
|
s |
t |
u |
d |
e |
n |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
密匙为___________________.
(3) 若下面即是那段包含地点(Midway)的破译不出的密文:
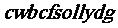
且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
w |
b |
c |
f |
s |
o |
l |
l |
y |
d |
g |
密匙为____________________,明文为_______________________.
20.(本题满分14分)
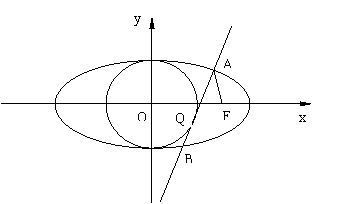
如图:已知椭圆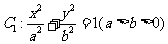 的内切圆
的内切圆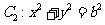 的一条切线交椭圆于A、B,且切线AB与圆的切点Q在
的一条切线交椭圆于A、B,且切线AB与圆的切点Q在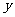 轴右侧.
轴右侧.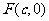 是椭圆的右焦点.
是椭圆的右焦点.
(1) 设点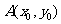 ,试用两点间距离公式推导
,试用两点间距离公式推导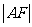 的表达式
的表达式
(用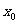 与
与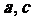 的式子表示);(7分)
的式子表示);(7分)
(2)判断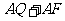 的长是否为定值?如果是定值,求出此定值;如果不是,请说明理由.(7分)
的长是否为定值?如果是定值,求出此定值;如果不是,请说明理由.(7分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com