
1.已知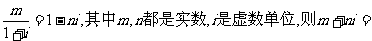 ( )
( )
A. B.
B.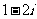 C.
C.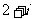 D.
D.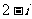
22.(本不题满分14分)设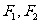 分别为椭圆
分别为椭圆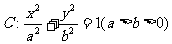 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ)若椭圆C上的点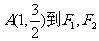 两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(Ⅱ)设点P是(Ⅰ)中所得椭圆上的动点,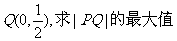 ;
;
(Ⅲ)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P在椭圆上任意一点,当直线PM、PN的斜率都存在,并记为KPM、KPN时,那么KPM与KPN之积是与点P位置无关的定值.试对双曲线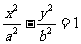 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
21.(本小题满分12分)已知数列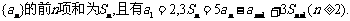
(Ⅰ)求数列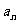 的通项公式;
的通项公式;
(Ⅱ)若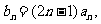 求数列
求数列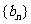 的前n项和
的前n项和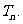
20.(本小题满分12分)某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元。
(Ⅰ)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(Ⅱ)设一次订购量为x个,零件的实际出厂单价为P元,写出函数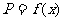 的表达式;
的表达式;
(Ⅲ)当销售商一次订购多少件时,该厂获得的利润为6000元?(工厂售出一个零件的利润=实际出厂单价-成本)
19.(本小题满分12分)如图所示,PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点;
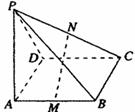 (Ⅰ)求证:MN//平面PAD;
(Ⅰ)求证:MN//平面PAD;
(Ⅱ)求证:MN⊥CD;
(Ⅲ)若二面角P-DC-A=45°,求证:MN⊥PDC.
18.(本小题满分12分)已知函数 处切线斜率为0.求:
处切线斜率为0.求:
(Ⅰ)a的值;
(Ⅱ)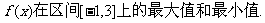
17.(本小题满分12分)已知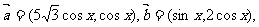 函数
函数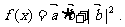
(Ⅰ)求函数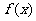 的最小正周期;
的最小正周期;
|
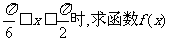 的值域.
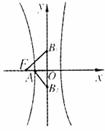
的值域.16.如图,双曲线C的中心在原点,虚轴两端点
分别为B1、B2,左顶点和左焦点分别为A、F,
若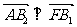 ,则双曲线C的离心率为
,则双曲线C的离心率为
.
15. 已知实数x、y满足条件
已知实数x、y满足条件 的最大值为
.
的最大值为
.
14.已知三棱锥O-ABC中,OA、OB、OC两两互相垂直,OC=1,OA=x,OB=y,若x+y=4,则三棱锥O-ABC体积的最大值是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com