
8. 上是增函数,若
上是增函数,若 ,则实数a的取值范围是
,则实数a的取值范围是
7.设
6.函数 的最小正周期为
的最小正周期为
5.在同一坐标系内,函数 的图象关于直线
的图象关于直线 对称,则
对称,则
。
4.已知 =
=
3.函数 的定义域是
的定义域是
2.已知集合 =
=
1.已知 ,那么p是q的
条件。
,那么p是q的
条件。
(从“充分非必要”、“必要非充分”、“充要或既不充分也不必要”中选取)
12.
 大家知道,在一次数学考试后,如果按顺序去掉一些低分,那末班级中的平均分提高,这个事实可以用数学语言描述为:
大家知道,在一次数学考试后,如果按顺序去掉一些低分,那末班级中的平均分提高,这个事实可以用数学语言描述为: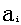 设表示第i个同学的数学考试成绩,若
设表示第i个同学的数学考试成绩,若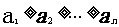 则
(结论用数学式子表示)
则
(结论用数学式子表示)
二 选择题
“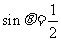 ”是”A=
”是”A=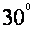 ”的
( )
”的
( )
A充分不必要条件B 必要不充分条件 C充分必要条件 D 既不充分也不必要条件
14 y=3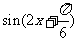 的函数的图像的一个对称中心是A
的函数的图像的一个对称中心是A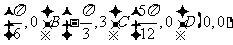
15 下列函数中既在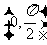 上为增函数又是以
上为增函数又是以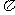 为最小正周期的偶函数的是( )
为最小正周期的偶函数的是( )
A y=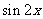 B y=
B y=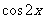 C y=
C y=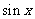 D
D 
16 把函数y=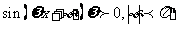 的图像向左平移
的图像向左平移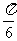 个单位,所得图像的解析式为y=
个单位,所得图像的解析式为y= 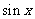 则
则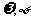 的值为( )
的值为( )
A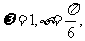 B
B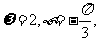 C
C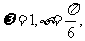 D
D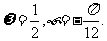
三 解答题
17 求函数y=2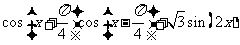 的值域和最小正周期.
的值域和最小正周期.
18
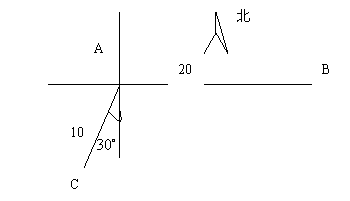 如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告诉在甲船的南偏西
如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告诉在甲船的南偏西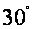 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到
,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到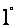 ).
).
19
已知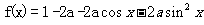 函数的最
函数的最
小值为
|
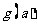 ,a
,a 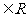 ;
;
①
求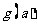
②
若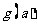 =
=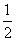 ,求a及此时
,求a及此时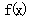 的最大值。
的最大值。
20
已知函数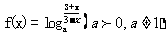
① 求函数的定义域
②判断的奇偶性并证明
③
求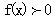 使x的的取值范围.
使x的的取值范围.
21某商场预计全年分批采购每台价值2400元的电视机共台,每批都购入x台(x为正整数),且每批均须付运输费元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运输费)成正比,若每批购入400台,则全年需用去运输和保管总费用43600元,现在全年只有不超过25000元的资金可以用于支付这批费用,请问,能否恰当地安排每批进货的数量,使资金购用?写出你的结论并说明理由。
21
已知函数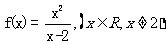
(1) 求函数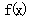 的单调区间
的单调区间
(2) 若函数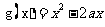 与函数
与函数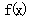 在
在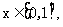 时有相同的值域,求a的值
时有相同的值域,求a的值
设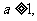 函数
函数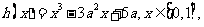 若对于任意
若对于任意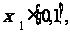 总存在
总存在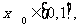 使得a
使得a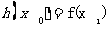 成立,求a的取值范围 .
成立,求a的取值范围 .
11.已知定义在上的偶函数满足条件;
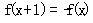 且在
且在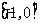 上是增函数;给出下面关于
上是增函数;给出下面关于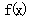 的命题:①
的命题:①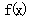 是周期函数;②
是周期函数;②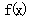 的图像关于直线x=1对称;③
的图像关于直线x=1对称;③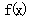 在
在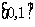 上是增函数;④在
上是增函数;④在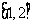 上是减函数;⑤
上是减函数;⑤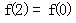 。其中正确的命题序号是
(请填上所有正确命题的序号)
。其中正确的命题序号是
(请填上所有正确命题的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com