
12.设an是fn(x)=(1+x)n+1(n∈N*)的展开式中xn项的系数,则an= ;数列{an}的前n项和为 .
11.在△ABC中,若tanAtanB=1,则sin(C-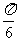 )= .
)= .
10.函数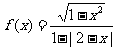 的定义域为
.
的定义域为
.
9.若{an}为等差数列,且a2+a3+a10+a11=48,则a6+a7等于 .
8.在数列{an}中,对任意n∈N*,都有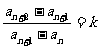 (k为常数),则称
(k为常数),则称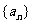 为“等差比
为“等差比
数列”,下面对“等差比数列”的判断:①k不可能为0;②等差数数列一定是等差比数
列;③等比数数一定是等差比数列;④通项公式为an=a·bn+c(a≠0,b≠0,1)的数列一
定是等差比数列,其中正确的判断 ( )
A.①② B.②③ C.③④ D.①④
第Ⅱ卷(共110分)
7.若底面边长为a的正四棱锥的全面积与棱长为a的正方体的全面积相等,那么这个正四棱锥的侧棱与底面所成角的余弦值为 ( )
A.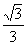 B.
B.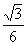 C.
C.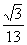 D.
D.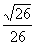
6.在2006年北京国际汽车展上,某汽车生产厂家准备推出10款不同的轿车参加车展,若
主办主只能为该厂提供6个展位,每个展位摆放一辆车,且甲、乙两款车不能摆放在2
号展位上,则该厂家展轿车的不同摆放方案有 ( )
A.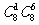 种 B.
种 B.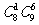 种 C.
种 C.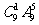 种 D.
种 D.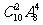 种
种
5.已知函数f(x)=ax3+bx2+cx+d(a≠0),当x=1时有极大值4,当x=3时有极小值0,且函数
图象过原点,则f(x)的表达式为 ( )
A.x3+6x2+9x B.x3-6x2-9x
C.x3-6x2+9x D.x3+6x2-9x
4.若函数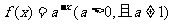 是定义域为R上的减函数,则函数
是定义域为R上的减函数,则函数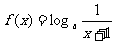
的图象是 ( )
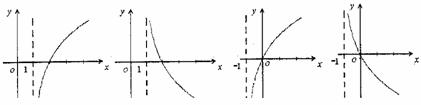
A. B. C. D.
3.若条件p: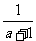 >1,条件q:a<0,则p是q的 ( )
>1,条件q:a<0,则p是q的 ( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com