21．(本小题满分12分)

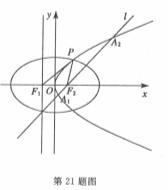
如图，设抛物线C₁:y²=4mx(m>0)的准线与x轴交于F₁，抛物线的焦点为F₂．以F₁、F₂为焦点，离心率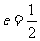的椭圆C₂与抛物线C₁的一个交点为P．

(1)当m=1时，直线L经过椭圆C₂的右焦点F₂与抛物线C_l交于A_l、A₂。两点，如果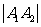等

于△PF_l F₂的周长，求直线L的斜率；

(2)求最小实数m，使得△PF_l F₂各边长均是正整数．

20．(本题满分12分)

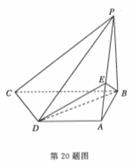
斯棱锥P－ABCD中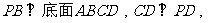，底面ABCD 为直角梯形，AD//BC,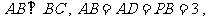点E在棱PA上，　　 且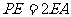

(1)求异面直线PA与CD的夹角；

(2)求证PC//平面EBD

(3)求平面ABE与平面BDE所夹的角A-BE-D的余弦值

19．(本题满分12分)

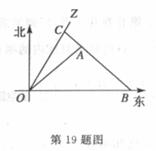
如图，一科学考察船从港口O出发，沿北偏东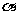角的射线OZ方向航行，而在离港口O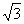海里的北偏东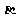角的A处有一个供给科考船物资的小岛，其中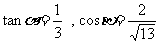．现指挥部需要紧急征调沿海岸线港口O正东m海里的B处的补给船，速往小岛A装运物资供给科考船．该船沿BA方向全速追赶科考船，并在C处相遇．经测算当两船运行的航线与海岸线OB围成的三角形OBC的面积S最小时，这种补给最适宜．

(1)求S关于m的函数关系式S(m)；

(2)应征调m为何值处的船只，补给最适宜?

18．(本题满分12分)

已知定义域为R的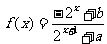函数是奇函数．

(1)求a，b的值。

(2)若对任意的t∈R，不等式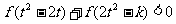恒成立，求实数k的取值范围．

17．(本题满分12分)

在△ABC中，角A、B、C的对边分别为a、b、c，且满足(2a-c)cosB=bcosC．

(1)求角B的大小；

(2)设向量m=(sinA，cos2A)，n=(4k,1)(k>1), m·n的最大值为5，求k的值．

16．如图，设平面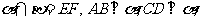垂足分别为B、D．若增加一个条件，就能推出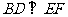．现有：

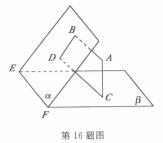①；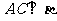

②AC与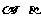的夹角相等；

③AC与CD在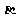内的射影在同一条直线上；

④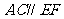

那么上述几个条件中能成为增加条件的是______ (填上你认为正确的所有答案序号)．

15．在平面内，三角形的面积为s，周长为C,则它的内切圆的半径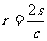．在空间中，三棱锥的体积为V，表面积为S，利用类比推理的方法，可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=________．

14． 已知向量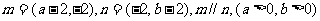,则ab的最小值是_____

13．已知函数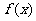是定义在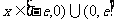上的奇函数，当

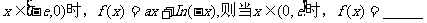
12．同时满足条件①函数图像成中心对称图形；②对任意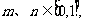若m≠n，有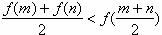的函数是

　 (A)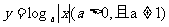　　 (B)y=cos2x

　 (C) 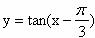　　　　　　　(D)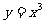

第Ⅱ卷　 (非选择题　 共90分)