
(17)(本小题满分12分)
已知数列{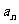 }是首项,
}是首项,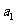 =4、公比
=4、公比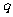 ≠1的等比数列,
≠1的等比数列,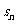 是其前n项和,且4
是其前n项和,且4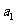 ,
,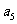 ,-2
,-2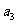 成等差数列.
成等差数列.
(I)求公比q的值;
(Ⅱ)求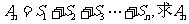 .
.
(18)(本小题满分12分))
已知函数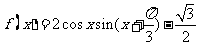
(I)求函数以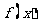 的最小正周期T;
的最小正周期T;
(Ⅱ)若△ABC的三边a,b,c满足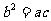 ,且边b所对的角为B,试求cosB的取值范围,并确定此时
,且边b所对的角为B,试求cosB的取值范围,并确定此时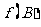 的最大值.
的最大值.
(19)(本小题满分12分)
某高等学校自愿献血的50位同学的血型分布情形如下表:
|
血型 |
A |
B |
AB |
O |
|
人数 |
20 |
10 |
5 |
15 |
(I)今从这50人中随机选出两人,问两人血型相同的概率是多少?
(Ⅱ)今有A血型的病人需要输血,从血型为A、O的同学中随机选出2人准备献血,记选择出A血型的人数为 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 ?
?
(20)(本小题满分12分)
一个多面体的直观图及三视图如图所示:(其中M、N别是AF、BC的中点).
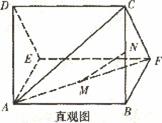 (I)求证:MN//平面CDEF;
(I)求证:MN//平面CDEF;
(Ⅱ)求二面角D-MN-B的余弦值绝对值.
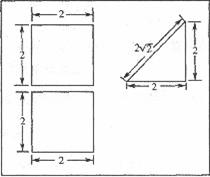
三视图
(21)(本小题满分12分)
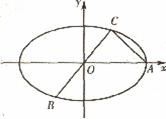
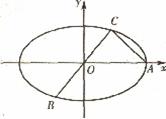
如图,已知A、B、C是椭圆E: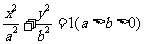 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为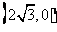 ,BC过椭圆的中心0,且AC⊥BC,
,BC过椭圆的中心0,且AC⊥BC,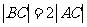 .
.
(I)求点C的坐标及椭圆E的方程;
 (Ⅱ)若椭圆E上存在两点P、Q,使∠PCQ的平分线总是垂直于x轴,试叛断向量
(Ⅱ)若椭圆E上存在两点P、Q,使∠PCQ的平分线总是垂直于x轴,试叛断向量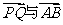 是否共线,并给出证明。
是否共线,并给出证明。
(22)(本小题满分14分)
已知函数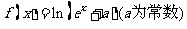 是实数集R上的奇函数,函数
是实数集R上的奇函数,函数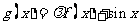 是区间[一1,1]上的减函数.
是区间[一1,1]上的减函数.
(I)求a的值;
(II) 若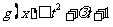 在x∈[一1,1]上恒成立,求t的取值范围.
在x∈[一1,1]上恒成立,求t的取值范围.
(Ⅲ) 讨论关于x的方程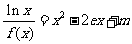 的根的个数。
的根的个数。
 (13)已知二项式
(13)已知二项式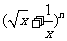 的展开式的第6项为常数项,则n=
的展开式的第6项为常数项,则n=
(14)在Rt△ABC中,∠C=90°,∠A=30°,则以A、B为焦点,过点C的椭圆的离心率是
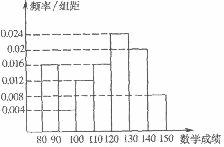
(15)某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图).则这10000人中数学成绩在[140,150]段的约是 。
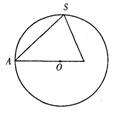 (16)已知三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为 .
(16)已知三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为 .
(1)复数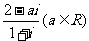 是纯虚数,则
是纯虚数,则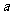 =
=
(A)0 (B)1 (C)2 (D)3
(2)抛物线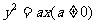 的焦点到其准线的距离是
的焦点到其准线的距离是
(A)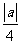 (B)
(B)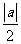 (c)
(c)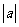 (D)
(D)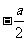
(3)用二分法研究函数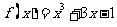 的零点时,第一次经计算
的零点时,第一次经计算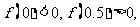 可得其中一个零点
可得其中一个零点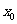 ∈ ,第二次应计算
.以上横线上应填的内容为
∈ ,第二次应计算
.以上横线上应填的内容为
(A)(0,0.5),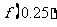 (B)(0,1),
(B)(0,1),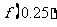
(C)(0.5,1),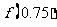 D)(0,0.5),
D)(0,0.5),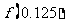
(4)若函数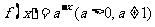 是定义域为R的增函数,则函数
是定义域为R的增函数,则函数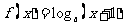 的图象大致是
的图象大致是
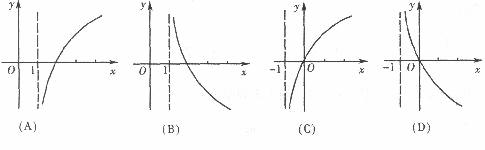
(5)已知a,b表示直线,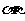 表示平面,则a∥
表示平面,则a∥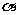 的一个充分条件是
的一个充分条件是
(A)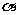 //
//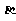 ,
,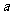 //
//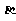 (B)
(B)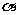 ⊥
⊥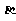 ,
,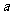 ⊥
⊥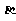
(C)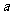 //
//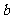 ,
,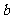 //
//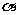 (D)
(D)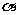
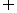
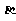 =
=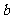 ,
,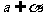 ,
,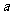 //
//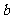
(6)过抛物线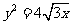 的焦点,且与圆
的焦点,且与圆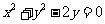 相切的直线方程是
相切的直线方程是
(A)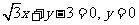
(B)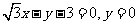
(C)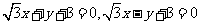
(D)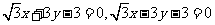
(7)已知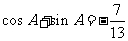 ,A为第四象限角,则ta
nA等于
,A为第四象限角,则ta
nA等于
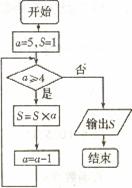 (A)
(A)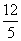 (B)
(B)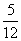 (C)
(C)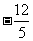 (D)
(D)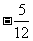
(8)右面的程序框图输出的结果是
(A)5
(B)10
(C)15
(D)20
(9)已知函数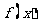 是以2为周期的偶函数,且当石
是以2为周期的偶函数,且当石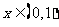 时,
时,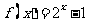 ,则
,则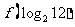 的值为
的值为
(A)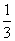 (B)
(B) 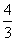 (C)2 (D)11
(C)2 (D)11
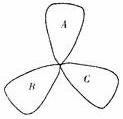 (10)荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如下图,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是
(10)荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如下图,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是
(A)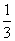 (B)
(B) 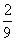
(C) 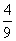 (D)
(D) 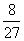
(11)已知等差数列{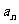 }的前n项和为
}的前n项和为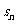 ,若
,若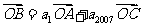 ,且A、B、C三点共线(0为该直线外一点),则
,且A、B、C三点共线(0为该直线外一点),则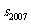 =
=
(A)2007 (B)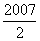 (C)
(C)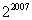 (D)
(D) 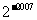
(12)点P是双曲线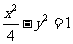 的右支上一点,M、N分别是圆
的右支上一点,M、N分别是圆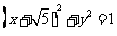 和圆
和圆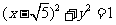 上的点,则
上的点,则 的最大值是
的最大值是
(A)2 (B)4 (C)6 (D)8
第Ⅱ卷 (非选择题共90分)
(17)(本小题满分12分)
已知数列{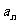 }是首项,
}是首项,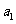 =4、公比
=4、公比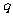 ≠1的等比数列,
≠1的等比数列,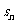 是其前n项和,且4
是其前n项和,且4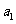 ,
,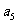 ,-2
,-2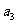 成等差数列.
成等差数列.
(I)求公比q的值;
(Ⅱ)求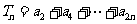 的值.
的值.
(18)(本小题满分12分))
已知函数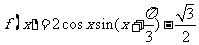
(I)求函数以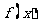 的最小正周期T;
的最小正周期T;
(U)在给定的坐标系中,用“五点法”作出函数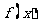 在一个周期上的图象.
在一个周期上的图象.

(19)(本小题满分12分)
甲乙两人玩一种游戏,每次由甲、乙各出1到5根手指头,若和为偶数算甲赢,否则算乙赢.
(I)若以A表示和为6的事件,求P(A);
(Ⅱ)现连玩三次,若以B表示甲至少赢一次的事件,C表示乙至少赢两次的事件,试问B与C是否为互斥事件?为什么?
(Ⅲ)这种游戏规则公平吗?试说明理由.
(20)(本小题满分12分)
一个多面体的直观图及三视图如图所示:(其中M、N别是AF、BC的中点).
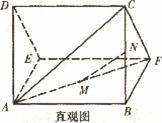 (I)求证:MN//平面CDEF;
(I)求证:MN//平面CDEF;
(Ⅱ)求多面体A-CDEF的体积.
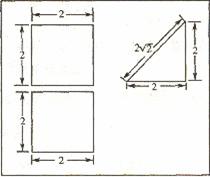
三视图
(21)(本小题满分12分)
如图,已知A、B、C是椭圆E: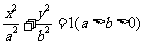 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为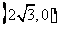 ,BC过椭圆的中心0,且AC⊥BC,
,BC过椭圆的中心0,且AC⊥BC,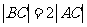 .
.
(I)求点C的坐标及椭圆E的方程;
 (Ⅱ)若椭圆E上存在两点P、Q,使得直线PC与直线QC关于直线
(Ⅱ)若椭圆E上存在两点P、Q,使得直线PC与直线QC关于直线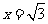 对称,求直线PQ的斜率.
对称,求直线PQ的斜率.
(22)(本小题满分14分)
已知函数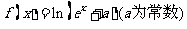 是实数集R上的奇函数,函数
是实数集R上的奇函数,函数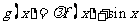 是区间[一1,1]上的减函数.
是区间[一1,1]上的减函数.
(I)求a的值;
(II)求A的取值范围;
(Ⅲ)若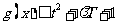 在x∈[一1,1]上恒成立,求t的取值范围.
在x∈[一1,1]上恒成立,求t的取值范围.
 (13)某公共汽车站每隔10分钟就有一趟车经过,小王随机赶到车站,则小王等车时间不超过4分钟的概率是
(13)某公共汽车站每隔10分钟就有一趟车经过,小王随机赶到车站,则小王等车时间不超过4分钟的概率是
(14)在Rt△ABC中,∠C=90°,∠A=30°,则以A、B为焦点,过点C的椭圆的离心率是
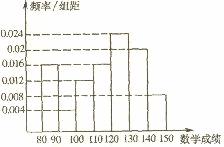
(15)某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图).则这10000人中数学成绩在[140,150]段的约是 。
 (16)一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于 cm3.
(16)一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于 cm3.
(1)复数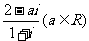 是纯虚数,则
是纯虚数,则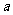 =
=
(A)0 (B)1 (C)2 (D)3
(2)抛物线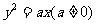 的焦点到其准线的距离是
的焦点到其准线的距离是
(A)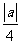 (B)
(B)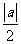 (c)
(c)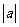 (D)
(D)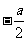
(3)用二分法研究函数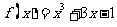 的零点时,第一次经计算
的零点时,第一次经计算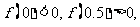 可得其中一个零点
可得其中一个零点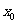 ∈ ,第二次应计算
.以上横线上应填的内容为
∈ ,第二次应计算
.以上横线上应填的内容为
(A)(0,0.5),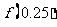 (B)(0,1),
(B)(0,1),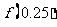
(C)(0.5,1),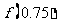 D)(0,0.5),
D)(0,0.5),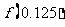
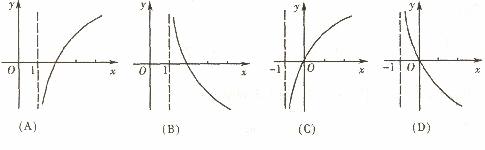
(4)若函数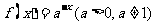 是定义域为R的增函数,则函数
是定义域为R的增函数,则函数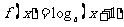 的图象大致是
的图象大致是
(5)已知a,b表示直线,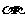 表示平面,则a∥
表示平面,则a∥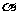 的一个充分条件是
的一个充分条件是
(A) //
//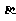 ,
,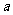 //
//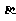 (B)
(B)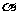 ⊥
⊥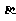 ,
,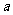 ⊥
⊥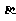
(C)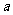 //
//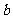 ,
,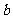 //
//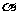 (D)
(D)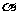
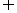
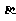 =
=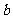 ,
,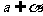 ,
,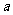 //
//
(6)过抛物线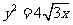 的焦点,且与圆
的焦点,且与圆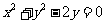 相切的直线方程是
相切的直线方程是
(A)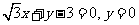
(B)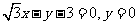
(C)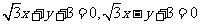
(D)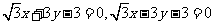
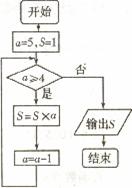
(7)已知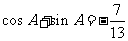 ,A为第四象限角,则ta
nA等于
,A为第四象限角,则ta
nA等于
 (A)
(A)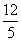 (B)
(B)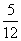 (C)
(C)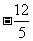 (D)
(D)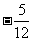
(8)右面的程序框图输出的结果是
(A)5
(B)10
(C)15
(D)20
(9)已知函数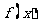 是以2为周期的偶函数,且当石
是以2为周期的偶函数,且当石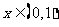 时,
时,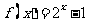 ,则
,则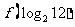 的值为
的值为
(A)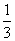 (B)
(B) 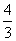 (C)2 (D)11
(C)2 (D)11
(10)设0<a<b<1,且a+b=1,给出下列结论:
①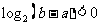 ②
②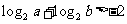
③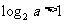 ④
④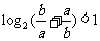
其中正确结论的个数是
(A)1个 (B)2个 (C)3个 (D)4个
(11)已知等差数列{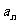 }的前n项和为
}的前n项和为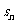 ,若
,若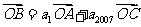 ,且A、B、C三点共线(0为该直线外一点),则
,且A、B、C三点共线(0为该直线外一点),则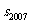 =
=
(A)2007 (B)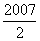 (C)
(C)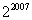 (D)
(D) 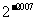
(12)点P是双曲线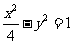 的右支上一点,M、N分别是圆
的右支上一点,M、N分别是圆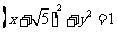 和圆
和圆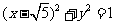 上的点,则
上的点,则 的最大值是
的最大值是
(A)2 (B)4 (C)6 (D)8
第Ⅱ卷 (非选择题共90分)
20.已知数列{an}满足a1=4,an=4-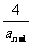 (n≥2),令bn=
(n≥2),令bn=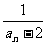 .
.
(1)求证数列{bn}是等差数列;(2)求数列{an}的通项公式.
21(本小题满分12分).已知函数f(x)=ln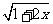 +mx。
+mx。
⑴f(x)为定义域上的单调函数,求实数m的取值范围;
⑵当m=–1时,求函数f(x)的最大值;
⑶当m=1,且1³a>b³0,证明: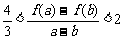 .
.
22(本小题满分14分).x轴上有一列点P1,P2,P3,…,Pn,…,已知当 时,点Pn是把线段Pn-1 Pn+1作n等分的分点中最靠近Pn+1的点,设线段P1P2,P2P3,…,Pn Pn+1的长度分别为a1,a2,a3,…,an,其中a1=1.
时,点Pn是把线段Pn-1 Pn+1作n等分的分点中最靠近Pn+1的点,设线段P1P2,P2P3,…,Pn Pn+1的长度分别为a1,a2,a3,…,an,其中a1=1.
(1)写出a2,a3和an( ,
,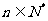 )的表达式;
)的表达式;
(2)证明:a1+a2+a3+…+an<3(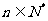 );
);
(3)设点.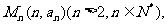 在这些点中是否存在两个点同时在函数
在这些点中是否存在两个点同时在函数
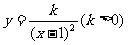 的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.
的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.
18、(本题满分12分)
已知空间向量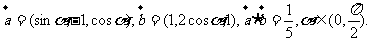
(I)求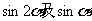 、
、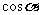 的值;
的值;
(II)设函数 R),指出
R),指出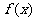 的最小正周期并求
的最小正周期并求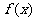 取得最大值时的x的值.
取得最大值时的x的值.
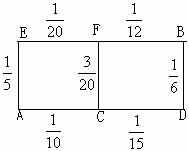 19(本小题12分).某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A
19(本小题12分).某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A C
C D算作两个路段:路段AC发生堵车事件的概率为
D算作两个路段:路段AC发生堵车事件的概率为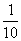 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为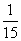 ).
).
(1) 请你为其选择一条由A到B的路线,使得
途中发生堵车事件的概率最小;
(2) 若记ξ路线A C
C F
F B中遇到堵车
B中遇到堵车
次数为随机变量ξ,求ξ的数学期望Eξ.
17、(本题满分12分)
已知集合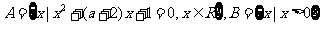 ,并且满足
,并且满足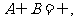
求实数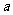 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com