
2.已知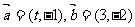 ,若
,若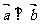 ,则实数t
= ( )
,则实数t
= ( )
A. B.
B.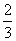 C.
C.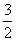 D.
D.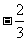
1.已知全集I = R,集合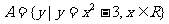 ,则A = ( )
,则A = ( )
A.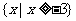 B.
B.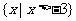
C.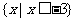 D.
D.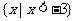
22.[14分]已知函数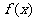 满足
满足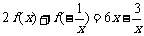 ,对任意x≠0恒成立,在数列{an}、{bn}中,
,对任意x≠0恒成立,在数列{an}、{bn}中,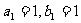 ,对任意
,对任意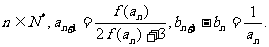
(1)求函数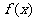 的解析式;
的解析式;
(2)求数列{an}与{bn}的通项公式;
(3)若对任意实数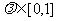 ,总存在自然数k,当
,总存在自然数k,当 时,
时,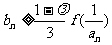 恒成立,求k的最小值.
恒成立,求k的最小值.
21.[12分]已知函数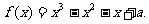
(1)确定函数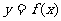 在哪个区间内是增函数;
在哪个区间内是增函数;
(2)若函数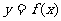 在图象与x轴恰好有三个交点,求实数a的取值范围.
在图象与x轴恰好有三个交点,求实数a的取值范围.
20.[12分]某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/102kg)与上市时间t(单位:天)的数据如下:
|
时间/t |
50 |
110 |
250 |
|
种植成本Q |
150 |
108 |
150 |
(1)根据上表数据,从下列函数中选取一个函数模型描述西红柿种植成本Q与上市时间t的变化关系: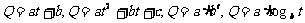 ,并说明选取的理由;
,并说明选取的理由;
(2)利用您选取的函数模型,求西红柿种植成本最低时的上市天数及最低种植成本.
19.[12分]已知等差数列{an}的首项a1 =1,公差d > 0,且a2 、a5 、a14恰好是等比数列{bn}的第1项、第2项、第3项.
(1)求数列{an}与{bn}的通项公式;
(2)若数列{cn}对于任意自然数n均有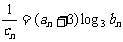 ,记{cn}的前n项和为Sn,求
,记{cn}的前n项和为Sn,求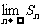 的值.
的值.
18.[12分]在△ABC中,三个内角A、B、C满足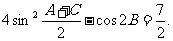
(1)求角B的度数;
(2)求函数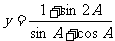 的值域.
的值域.
17.[12分]已知p: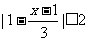 ,q:
,q: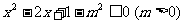 ,若﹁p是﹁q的充分不必要条件,求实数m的取值范围;
,若﹁p是﹁q的充分不必要条件,求实数m的取值范围;
16.图中一组函数图像,它们分别与其后所列的一个现实情境相匹配:
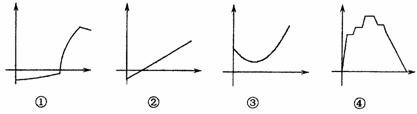
情境A:一份30分钟前从冰箱里取出来,然后被放到微波炉里加热,最后放到餐桌上的食物的温度(将0时刻确定为食物从冰箱里被取出来的那一刻);
情境B:一个1970年生产的留声机从它刚开始的售价到现在的价值(它被一个爱好者收藏,并且被保存得很好);
情境C:从你刚开始放水洗澡,到你洗完后把它排掉这段时间浴缺里水的高度;
情境D:根据乘客人数,每辆公交车一趟营运的利润;
其中情境A、B、C、D分别对应的图象是 .
15.函数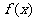 的反函数
的反函数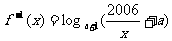 ,其中a >
0,则方程
,其中a >
0,则方程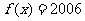 的解为
.
的解为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com