
2.设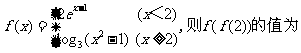
A.0 B.1 C.2 D.3
1.若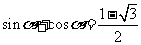 ,则
,则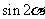 =
=
A.
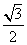 B.
-
B.
-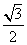 C.
C. 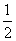 D. -
D. -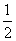
20.(本小题满分14分)
由坐标原点O向函数y=x3-3x2的图象W引切线l1,切点为P1(x1,y1)(P1,O不重合),再由点P1引W的切线l2,切点为P2(x2,y2)(P1,P2不重合),…,如此继续下去得到点列{Pn(xn,yn)}.
(Ⅰ)求x1的值;
(Ⅱ)求xn与xn+1满足的关系式;
(Ⅲ)求数列{xn}的通项公式.
19.(本小题满分14分)
设x,y∈R,i,j为直角坐标平面内x,y轴正方向上的单位向量,若a=(x+1)i+yj,
b=(x-1)i+yj , |a|+|b|=4.
(Ⅰ)求点M(x,y)的轨迹C的方程;
(Ⅱ)过点(0, m)作直线l与曲线C交于A,B两点,若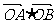 =0,求m的取值范
=0,求m的取值范
围.
18.(本小题满分13分)
设函数f(x)=-4x+b,且不等式|f(x)|<k的解集为{x|-1<x<2}.
(Ⅰ)求b,k的值;
(Ⅱ) 证明:函数 对称.
对称.
17.(本小题满分13分)
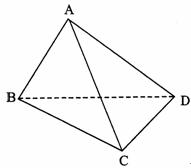
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
(Ⅰ)求证:BC⊥AD;
(Ⅱ)若点D到平面ABC的距离等于3,求二面角A-BC-D的正弦值;
(Ⅲ)设二面角A-BC-D的大小为θ,猜想θ为何值时,四面体ABCD的体积最大 。
16.(本小题满分13分)
学校组级别5名学生参加区级田赛运动会,规定每人在跳高、跳远、铅球3个项目中任选一项,假设5名学生选择哪个项目是等可能的.
(Ⅰ)求3个项目都有人选择的概率;
(Ⅱ)求恰有2个项目有人选择的概率.
15.(本小题满分13分)
已知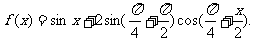
(Ⅰ)若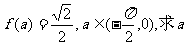 的值;
的值;
(Ⅱ)若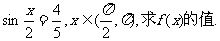
14.过圆x2+y2=8内的点P(-1,2)作直线l交圆于A、B两点,若直线l的倾斜角为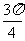 ,则弦AB的长为 ;弦AB被点P平分时,直线AB的方程为
.
,则弦AB的长为 ;弦AB被点P平分时,直线AB的方程为
.
13.在平面直角坐标中,由 ,所确定的平面区域的面积是 .
,所确定的平面区域的面积是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com