3．设A为圆(x+1)²+y²=4上的动点，PA是圆的切线，且|PA|=1，则P点的轨迹方程为

　 (A)(x+1)²+y²=25　　　　　　　　　　 了 　 (B)(x+1)²+y²=5

　 (C)x²+(y+1)²=25　　　　　　　　　　　　 (D)(x-1)²+y²=5

2．下列命题错误的是

　　(A)命题“若m>0，则方程x²+x-m=0有实数根”的逆否命题为：“若方程x²+x-m=0无实数根，则m≤0”．

　 (B)“x=1”是“x²-3x+2=0”的充分不必要条件．

　 (C)若pq为假命题，则p、q均为假命题．

　 (D)对于命题p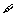：x∈R，使得x²+x+l<0，则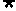p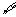：x∈R，均有x²+x+l≥0

1．若复数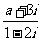(a∈R，i为虚数单位)是纯虚数，则实数a的值为

　　(A)-2　　　　　　 　　(B)4　　　　　　　 　(C)-6　　　　　　　 　(D)6

22．(本小题满分14分)

　 已知点Pn(a_n，b_n)满足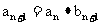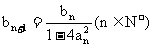，)，且点P₁的坐标为(1，-1)．　　

(I)求过点P₁，P₂的直线L的方程；

(Ⅱ)试用数学归纳法证明：对于n∈N^*，点P_n都在(I)中的直线L上；

(Ⅲ)试寻求使不等式(1+a₁)(1+a₂)…(1+a_n)≥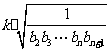所有n∈N^*成立的最大实数k．

21．(本小题满分12分)

　 已知椭圆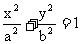 (a>b>0)，它的上下顶点分别是A、B，点M是椭圆上的动点(不与A、B重合)，直线AM交直线Y=2b于点N，且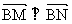

　(I)求椭圆的离心率；

　(II)若斜率为I的直线L交椭圆于P、Q两点，求证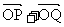：与向量a=(-3．1)共线(其中0为坐标原点)．

20．(本小题满分12分)

某地一水库年初有水量口(a≥10000)，其中含污染物的量为P。(设水与污染物混合均匀)已知该地降水量与月份的关系为；而每月流入水库的污水量与蒸发的水量都是r，且此污水中含污染物的量为p(p<r)，设当年水库中的水不作它用．

(I)求第x月水库中水的含污比g(x)的表达式(含污比=)；

(Ⅱ)当 p₀=0时，求水质最差的月份及此月的含污比。

19．(本小题满分12分)

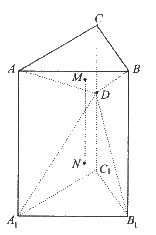
直三棱柱ABC-A₁B_lC_l中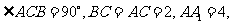，，D为棱CC_l上的一动点，M、N分别为△ABD、△A₁B₁D的重心．

　(I)求证：MN⊥AB；

　(Ⅱ)若二面角C-AB-D的正切值为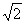，求二半平面ABD、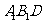所成锐二面角的余弦值；

　(Ⅲ)若点C₁在平面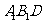上的射影正好为N，试判断C在平面ABD上的射影是否为M?并说明理由．

18．(本小题满分12分)。

已知函数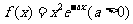，求函数在[1，2]上的最大值

17．(本小题满分12分)

已知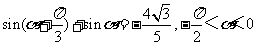，求cosa的值．

16．下列四个命题：

①若变量y与x之间的相关系数r=- 0.9362．查表得到相关系数临界值r_0.05=0．8013，则变量y与x之间具有线性相关关系；

②若a>0，b>0，则不等式a³+b³≥3ab²恒成立；

③对于函数f(x)=x²+mx+n，若f(a)>0，f(b)>0，则函数f(x)在(a，b)内至多有一个零点；

④y=f(x-2)和y=f(2-x)的图象关于x=2对称．

　　 其中正确命题的序号有________(填上所有正确命题的序号)．