
4.设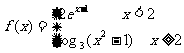 ,则
,则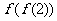 的值为
的值为
A.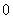 B.
B.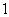 C.
C.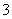 D.
D.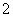
3.函数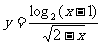 的定义域为
的定义域为
A.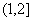 B.
B.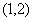 C.
C.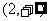 D.
D.
2.已知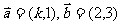 ,若
,若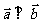 ,则
,则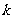 的值是
的值是
A.5 B.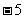 C.
C.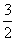 D.
D.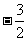
1.函数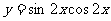 的最小正周期为
的最小正周期为
A.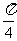 B.
B.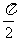 C.
C.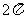 D.
D.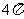
21.(本小题满分14分)我们在下面的表格内填写数值:先将第1行的所有空格填上1;再把一个首项为1,公比为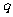 的数列
的数列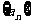 依次填入第一列的空格内;然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其它空格.
依次填入第一列的空格内;然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其它空格.
|
|
第1列 |
第2列 |
第3列 |
… |
第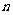 列 列 |
|
第1行 |
1 |
1 |
1 |
… |
1 |
|
第2行 |
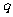 |
|
|
|
|
|
第3行 |
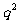 |
|
|
|
|
|
… |
… |
|
|
|
|
第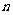 行 行 |
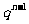 |
|
|
|
|
(1)设第2行的数依次为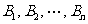 ,试用
,试用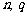 表示
表示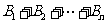 的值;
的值;
(2) 设第3列的数依次为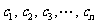 ,求证:对于任意非零实数
,求证:对于任意非零实数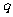 ,
,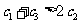 ;
;
(3)请在以下两个问题中选择一个进行研究 (只能选择一个问题,如果都选,被认为选择了第一问).
①能否找到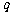 的值,使得(2) 中的数列
的值,使得(2) 中的数列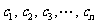 的前
的前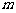 项
项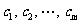
(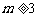 ) 成为等比数列?若能找到,m的值有多少个?若不能找到,说明理由.
) 成为等比数列?若能找到,m的值有多少个?若不能找到,说明理由.
②能否找到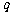 的值,使得填完表格后,除第1列外,还有不同的两列数的前三项各
的值,使得填完表格后,除第1列外,还有不同的两列数的前三项各
自依次成等比数列?并说明理由.
20.(本小题满分14分)已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点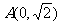 为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称. (1)求双曲线C的方程; (2)若Q是双曲线C上的任一点,F1、F2为双曲线C的左、右两个焦点,从F1引∠F1QF2的平分线的垂线,垂足为N,试求点N的轨迹方程; (3)设直线y=mx+1与双曲线C的左支交于A、B两点,另一直线L经过M(-2,0)及AB的中点,求直线L在y轴上的截距b的取值范围.
为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称. (1)求双曲线C的方程; (2)若Q是双曲线C上的任一点,F1、F2为双曲线C的左、右两个焦点,从F1引∠F1QF2的平分线的垂线,垂足为N,试求点N的轨迹方程; (3)设直线y=mx+1与双曲线C的左支交于A、B两点,另一直线L经过M(-2,0)及AB的中点,求直线L在y轴上的截距b的取值范围.
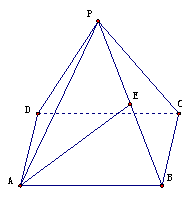
19.(本小题满分14分)如图所示,正四棱锥P-ABCD
中,侧棱PA与底面ABCD所成的角的正切值为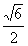
(1)求侧面PAD 与底面ABCD所成二面角的大小
(2)若E 是PB 中点,求异面直线PD与AE所成的
角的正切值 (3)在侧面PAD上寻找一点F使EF⊥
侧面PBC,试确定F的位置并证明.
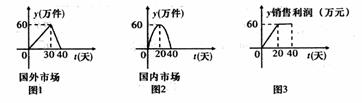
18.(本小题满分14分)某跨国公司是专门生产健身产品的企业,第一批产品A上市销售40天内全部售完,该公司对第一批产品A上市后的国内外市场销售情况进行调研,结果如图1、图2、图3所示。其中图1的折线表示的是国外市场的日销售量与上市时间的关系;图2的抛物线表示的是国内市场的日销售量与上市时间的关系;图3的折线表示的是每件产品A的销售利润与上市时间的关系.
(I)分别写出国外市场的日销售量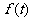 、国内市场的日销售量
、国内市场的日销售量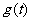 与第一批产品A上
与第一批产品A上
市时间t的关系式;
(II)第一批产品A上市后的哪几天,这家公司的日销售利润超过6300万元.
17.(本小题满分12分)口袋里装有大小相同卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为 .(Ⅰ)
.(Ⅰ) 为何值时,其发生的概率最大?说明理由;(Ⅱ)求随机变量
为何值时,其发生的概率最大?说明理由;(Ⅱ)求随机变量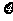 的期望E
的期望E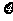 .
.
16.(本小题满分12分)在△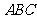 中,
中,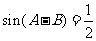 ,
,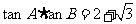 ,(1)求
,(1)求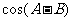 ;(2)求角
;(2)求角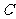 的大小.
的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com