
5.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,且直角边长为1,那么这个几何体的体积为
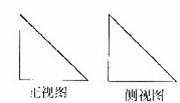
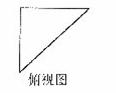
(A)1 (B)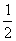 (C)
(C)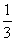 (D)
(D)
4.设直线过点(a,0),其斜率为-1,且与圆X2+Y2=2相切,则a的值为
(A)±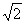 (B)±2 (C)±2
(B)±2 (C)±2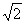 (D)±4
(D)±4
3.下列函数中周期为2的函数是
(A)y=2cos2πx-l (B)y=sin2πx+cos2πx
(C)y=tan(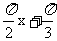 ) (D)y=sinπxcosπx
) (D)y=sinπxcosπx
2.命题“三角形中最多有一个内角是钝角”的否定是
(A)有两个内角是钝角 (B)有三个内角是钝角
(C)至少有两个内角是钝角 (D)没有一个内角是钝角
1.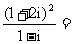
(A) 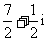 (B)
(B) 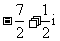 (C)
(C) 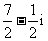 (D)
(D) 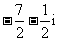
22.(本小题满分14分)
已知点Pn(an,bn)满足an+1=an·bn+1,bn+1=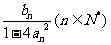 ,且点P1的坐标为(1,-1).
,且点P1的坐标为(1,-1).
(I)求过点P1,P2的直线l的方程;
(Ⅱ)试用数学归纳法证明:对于n∈N*,点Pn都在(I)中的直线l上;
(Ⅲ)试寻求使不等式(1+a1)(1+a2)…(1+an)≥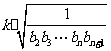 对所有n∈N*成立的最大实数k.
对所有n∈N*成立的最大实数k.
21.(本小题满分12分)
已知椭圆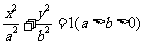 ,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线y=2b于点N,且
,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线y=2b于点N,且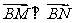 .
.
(I)求椭圆的离心率;
(Ⅱ)若斜率为1的直线l交椭圆于P、Q两点,求证: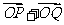 与向量a=(-3,1)共线(其中O为坐标原点).
与向量a=(-3,1)共线(其中O为坐标原点).
20.(本小题满分12分)
某地一水库年初有水量a(a≥10000),其中含污染物的量为p0(设水与污染物混合均匀),已知该地降水量与月份的关系为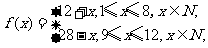 而每月流入水库的污水量与蒸发的水量都是r,且此污水中含污染物的量为p(p<r),设当年水库中的水不作它用.
而每月流入水库的污水量与蒸发的水量都是r,且此污水中含污染物的量为p(p<r),设当年水库中的水不作它用.
(I)求第x月水库中水的含污比g(x)的表达式(含污比= );
);
(Ⅱ)当p0=0时,求水质最差的月份及此月的含污比.
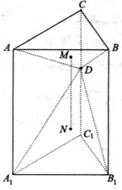
19.(本小题满分12分)
直三棱柱ABC-A1B1C1中,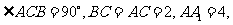 D为棱
D为棱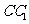 上的一动点,
上的一动点,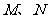 分别为
分别为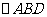 、
、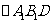 的重心.
的重心.
(I)求证: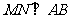 ;
;
(Ⅱ)若二面角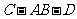 的正切值为
的正切值为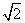 ,求二半平面
,求二半平面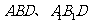 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)若点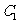 在平面
在平面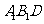 上的射影正好为N,试判断C在平面ABD上的射影是否为M?并说明理由.
上的射影正好为N,试判断C在平面ABD上的射影是否为M?并说明理由.
18.(本小题满分12分)
已知函数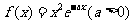 ,求函数在[1,2]上的最大值.
,求函数在[1,2]上的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com