
9.记首项为1、公比为q(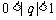 )的无穷等比数列
)的无穷等比数列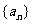 的各项的和为S,Sn表示该数列的前n项和,且
的各项的和为S,Sn表示该数列的前n项和,且 ,则实数
,则实数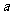 的取值范围为
的取值范围为
A.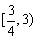 B.
B.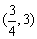
C.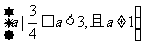 D.
D.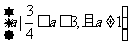
8.设离散型随机变量 可能的取值为1、2、3、4,
可能的取值为1、2、3、4,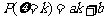 (
(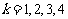 ),又
),又 的数学期望为
的数学期望为 ,则
,则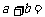
A.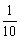 B.0 C.
B.0 C.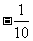 D.
D.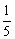
7.一个球的内接正四棱柱的侧面积与上下两底面积的和之比为4 : 1 , 体积为4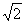 ,则这个球的表面积
,则这个球的表面积
A.12
B.12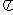 C.
C.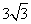
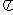 D.12
D.12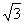
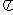
6.设椭圆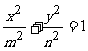 、双曲线
、双曲线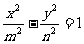 、抛物线
、抛物线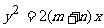 (其中
(其中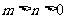 )的离心率分别为
)的离心率分别为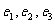 ,则
,则
A.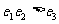 B.
B.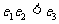
C.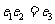 D.
D.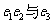 大小不确定
大小不确定
5.设地球的半径为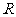 ,已知地球表面上A、B两地的纬度均为北纬
,已知地球表面上A、B两地的纬度均为北纬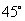 ,又A、B两地的球面距离为
,又A、B两地的球面距离为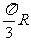 ,则A、B两地的经度差可以为
,则A、B两地的经度差可以为
A.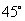 B.
B.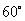 C.
C.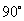 D.
D.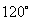
4.函数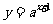 的图象与函数
的图象与函数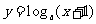 (其中
(其中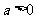 且
且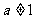 )的图象关于
)的图象关于
A.直线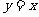 对称 B.直线
对称 B.直线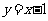 对称
对称
C.直线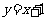 对称 D.直线
对称 D.直线 对称
对称
3.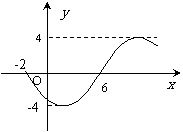 函数
函数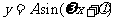 (
( >0,|
>0,|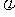 |<
|< 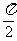 ,
,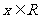 )的部 分图象如图所示,则此函数表达式为
)的部 分图象如图所示,则此函数表达式为
A.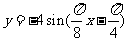
B.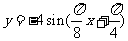
C.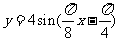
D.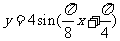
2.利用数学归纳法证明不等式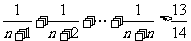 时,由k递推到k+1左边应添加的因式是
时,由k递推到k+1左边应添加的因式是
A.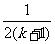 B.
B.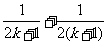
C.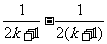 D.
D.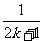
1.条件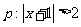 ,条件
,条件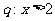 ,则
,则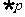 是
是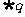 的
的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
22.(本小题满分14分)
已知抛物线的顶点在原点,焦点在y轴的负半轴上,过其上一点P(x0,y0)(x0≠0)的切线方程为y-y0=2ax0(x-x0)(a为常数)
(I)求抛物线方程;
(Ⅱ)斜率为k1的直线PA与抛物线的另一交点为A,斜率为k2的直线PB与抛物线的另一交点为B(A、B两点不同),且满足k2+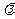 k1=0(
k1=0(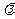 ≠0,
≠0,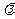 ≠-1),若
≠-1),若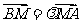 ,求证线段PM的中点在y轴上;
,求证线段PM的中点在y轴上;
(Ⅲ)在(Ⅱ)的条件下,当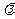 =1,k1<0时,若P的坐标为(1,-1),求
=1,k1<0时,若P的坐标为(1,-1),求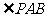 为钝角时点A的纵坐标的取值范围.
为钝角时点A的纵坐标的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com