
(17)(本小题满分12分)
求以坐标原点为顶点,坐标轴为对称轴且经过点A(2,-4)的抛物线的方程.
(18)(本小题满分12分)
已知函数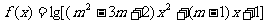 的定义域为R,求实数m的取值范围。
的定义域为R,求实数m的取值范围。
(19)(本小题满分12分)
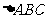 中,BC=a,AB=c,AC=b,且向量m=(b,b-
中,BC=a,AB=c,AC=b,且向量m=(b,b-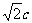 ),n=(tanA,tanB),
),n=(tanA,tanB),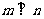 ,求角A的值。
,求角A的值。
(20)(本小题满分12分)
据统计,某市的工业垃圾若不回收处理,每吨约占地4平方米.2002年,环保部门共回收处理了100吨工业垃圾,且以后垃圾回收处理量每年递增20%(工业垃圾经回收处理后,不再占用土地面积).
(I)2007年能回收处理多少吨工业垃圾?(精确到1吨)
(Ⅱ)从2002年到2015年底,可节约土地多少平方米(精确到lm。)?
(参考数据1.24≈2.1 1.25≈2.5 1.26≈3.0 1.213≈10.7 1.214≈12.8)
(21)(本小题满分12分)
已知点A(-l,O),点B(1,O),动点C满足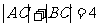
(I)求点C的轨迹方程;
(Ⅱ)设过点A和点D(O,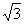 )的直线为L,L与点C的轨迹交于点P(不同于点A),
)的直线为L,L与点C的轨迹交于点P(不同于点A),
若求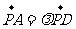 ,求
,求 的值.
的值.
(22)(本小题满分14分)
已知数列{an}中,a1=l,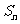 { an }的前n项和,当n≥2时,
{ an }的前n项和,当n≥2时,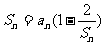 .
.
(I)求证{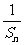 }是等差数列;
}是等差数列;
(Ⅱ)若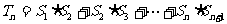 ,求Tn;
,求Tn;
(Ⅲ)在条件(Ⅱ)下,试求满足不等式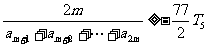 的正整数m.
的正整数m.
(13)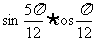 =--.
=--.
(14)与双曲线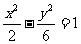 有共同渐近线,并且与椭圆
有共同渐近线,并且与椭圆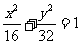 有相同焦点的双曲线的方程为__________________
有相同焦点的双曲线的方程为__________________
(15)等差数列{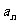 }中,a1=20,前n项和为
}中,a1=20,前n项和为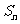 ,且S10=S15,则当n取______时,
,且S10=S15,则当n取______时,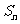 有最大值。
有最大值。
(16)给出下列命题:
①如果一个命题的否命题是真命题,那么这个命题的逆命题也是真命题;
②若。a>b>0,c>d>o,则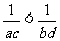 ;
;
③若一个数列的前n项和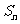 =
=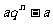 (a,q为非零常数,n∈N+),那么这个数列一定是等比数列
(a,q为非零常数,n∈N+),那么这个数列一定是等比数列
④过点P(2,2)与抛物线y2=2x只有一个公共点的直线有2条.
其中正确命题的序号是_______(把你认为正确命题的序号都填上)
(1)命题p: x>l,log2x>0,则
x>l,log2x>0,则 p是
p是
(A)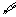 x >1,log2x≤O (B)
x >1,log2x≤O (B) 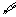 x≤l,log2x
>0
x≤l,log2x
>0
(C) 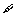 x>l,log2x≤O (D)
x>l,log2x≤O (D) 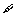 x≤l,log2x
>0
x≤l,log2x
>0
(2)“△ABC有一个内角是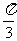 ”是“△ABC三个内角可构成等差数列”的
”是“△ABC三个内角可构成等差数列”的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(3)给出下列结论
①a>b c-a<c-b ②a>b>0
c-a<c-b ②a>b>0 ac2>bc2
ac2>bc2
③ a>b,c>b a-c>b-d ④a>b>0,c>d>0
a-c>b-d ④a>b>0,c>d>0
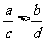
则上述结论中,正确的结论个数是
(A)1 (B)2 (C)3 (D)4
(4)已知a·b<0,则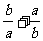 有
有
(A)最小值2 (B)最小值-2 (C)最大值-2 (D)最大值2
(5)方程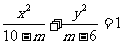 表示椭圆,则m的取值范围是
表示椭圆,则m的取值范围是
(A)(6,10) (B)(8,10)
(C)(6,8) (D)(6,8) ∪(8,10)
(6)在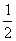 和8之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积为
和8之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积为
(A)8 (B)±8 (C)16 (D)±16
(7)关于x的不等式ax-b<0的解集为(-∞,1),则关于x的不等式(ax+b)(x-2)<0的解集为
(A)(-∞,-1) ∪(2,+∞) (B)(-1,2)
(C)(1,2) (D)(-∞,1)∪(2,+∞)
(8)实数x,y满足不等式组 ,则t=2y-3x的最大值是
,则t=2y-3x的最大值是
(A)-3 (B)-2 (C)0 (D)不存在
(9)抛物线x2=ay上的点与定点P(o,a)的距离的最小值是
(A) (B)
(B)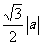
(C) 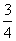 a2 (D)
a2 (D)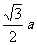
(10)已知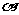 、
、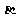 均为锐角,cos(
均为锐角,cos( )=
)=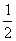 ,sin(
,sin( )=-
)=-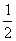 , cos2
, cos2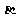 =
=
(A) 0 (B)
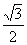 (C) -
(C) -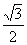 (D)-
(D)-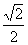
(11)一艘轮船按照北偏西500的方向,以15里每小时的速度航行,一个灯塔M原来在 轮船的北偏东100方向上.经过40分钟,轮船与灯塔的距离是5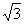 里,则灯塔和轮船原来的距离为
里,则灯塔和轮船原来的距离为
(A)2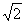 里
(B)3里 (C)4里
(D)5里
里
(B)3里 (C)4里
(D)5里
(12)已知F1、F2是椭圆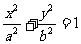 (a>b>0)的两个焦点,点P在椭圆上,且
(a>b>0)的两个焦点,点P在椭圆上,且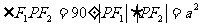 该椭圆的离心率为
该椭圆的离心率为
(A) 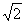 (B)
(B) 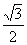 (C)
(C) 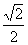 (D)
(D) 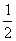
第Ⅱ卷 (非选择题共90分)
(17)(本小题满分12分)
已知函数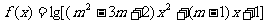 的定义域为R,求实数m的取值范围。
的定义域为R,求实数m的取值范围。
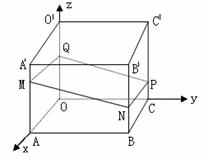
(18)(本小题满分12分)
如图,建立空间直角坐标系Oxyz,棱长为2的正方体OABCD-O′A′B′C′被一平面截得四边形MNPQ,其中N、Q分别是BB′、OO′的中点,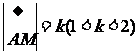 ,且
,且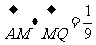 。
。
(1)求k的值
(2)求cos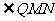 .
.
(19)(本小题满分12分)
 中,BC=a,AB=c,AC=b,且向量m=(b,b-
中,BC=a,AB=c,AC=b,且向量m=(b,b-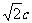 ),n=(tanA,tanB),
),n=(tanA,tanB),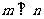 ,求角A的值。
,求角A的值。
(20)(本小题满分12分)
据统计,某市的工业垃圾若不回收处理,每吨约占地4平方米.2002年,环保部门共回收处理了100吨工业垃圾,且以后垃圾回收处理量每年递增20%(工业垃圾经回收处理后,不再占用土地面积).
(I)2007年能回收处理多少吨工业垃圾?(精确到1吨)
(Ⅱ)从2002年到2015年底,可节约土地多少平方米(精确到lm。)?
(参考数据1.24≈2.1 1.25≈2.5 1.26≈3.0 1.213≈10.7 1.214≈12.8)
(21)(本小题满分12分)
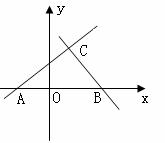
已知过点A(-2,0)的斜率为k1的直线,与过点B(2,0)斜率为k2的直线交于点C,且k1k2=-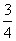
(1)求点C的轨迹方程
(2)设过点P(-4,0)且与点C的轨迹相切于点E的直线为L,L交y轴于点M,若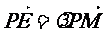 ,求
,求 得值
得值
(22)(本小题满分14分)
已知数列{an}中,a1=l,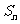 { an }的前n项和,当n≥2时,
{ an }的前n项和,当n≥2时,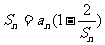 .
.
(I)求证{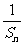 }是等差数列;
}是等差数列;
(Ⅱ)若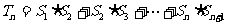 ,求Tn;
,求Tn;
(Ⅲ)在条件(Ⅱ)下,试求满足不等式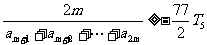 的正整数m.
的正整数m.
(13)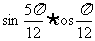 =--.
=--.
(14)与双曲线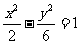 有共同渐近线,并且与椭圆
有共同渐近线,并且与椭圆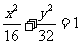 有相同焦点的双曲线的方程为__________________
有相同焦点的双曲线的方程为__________________
(15)等差数列{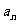 }中,a1=20,前n项和为
}中,a1=20,前n项和为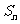 ,且S10=S15,则当n取______时,
,且S10=S15,则当n取______时,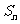 有最大值。
有最大值。
(16)给出下列命题:
①如果一个命题的否命题是真命题,那么这个命题的逆命题也是真命题;
②若。a>b>0,c>d>o,则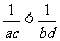 ;
;
③若一个数列的前n项和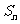 =
=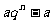 (a,q为非零常数,n∈N+),那么这个数列一定是等比数列
(a,q为非零常数,n∈N+),那么这个数列一定是等比数列
④过点P(2,2)与抛物线y2=2x只有一个公共点的直线有2条.
其中正确命题的序号是___________(把你认为正确命题的序号都填上)
(1)命题p: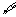 x>l,log2x>0,则
x>l,log2x>0,则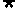 p是
p是
(A)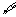 x >1,log2x≤O (B)
x >1,log2x≤O (B) 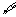 x≤l,log2x
>0
x≤l,log2x
>0
(C) 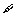 x>l,log2x≤O (D)
x>l,log2x≤O (D) 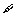 x≤l,log2x
>0
x≤l,log2x
>0
(2)“△ABC有一个内角是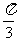 ”是“△ABC三个内角可构成等差数列”的
”是“△ABC三个内角可构成等差数列”的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(3)已知向量a=(1,0,1),b=(-1,0,2).且ka+b与2a-b互相垂直,则实数k的值是
(A)1 (B)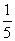 (C)
(C)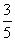 (D)
(D)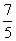
(4)已知a·b<0,则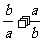 有
有
(A)最小值2 (B)最小值-2 (C)最大值-2 (D)最大值2
(5)方程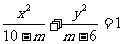 表示椭圆,则m的取值范围是
表示椭圆,则m的取值范围是
(A)(6,10) (B)(8,10)
(C)(6,8) (D)(6,8) ∪(8,10)
(6)在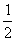 和8之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积为
和8之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积为
(A)8 (B)±8 (C)16 (D)±16
(7)关于x的不等式ax-b<0的解集为(-∞,1),则关于x的不等式(ax+b)(x-2)<0的解集为
(A)(-∞,-1) ∪(2,+∞) (B)(-1,2)
(C)(1,2) (D)(-∞,1)∪(2,+∞)
(8)实数x,y满足不等式组 ,则t=2y-3x的最大值是
,则t=2y-3x的最大值是
(A)-3 (B)-2 (C)0 (D)不存在
(9)抛物线x2=ay上的点与定点P(o,a)的距离的最小值是
(A) (B)
(B)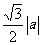
(C) 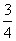 a2 (D)
a2 (D)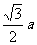
(10)已知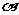 、
、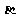 均为锐角,cos(
均为锐角,cos( )=
)=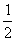 ,sin(
,sin( )=-
)=-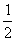 , cos2
, cos2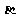 =
=
(A) 0 (B)
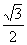 (C) -
(C) -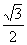 (D)-
(D)-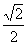
(11)一艘轮船按照北偏西500的方向,以15里每小时的速度航行,一个灯塔M原来在 轮船的北偏东100方向上.经过40分钟,轮船与灯塔的距离是5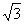 里,则灯塔和轮船原来的距离为
里,则灯塔和轮船原来的距离为
(A)2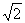 里
(B)3里 (C)4里
(D)5里
里
(B)3里 (C)4里
(D)5里
(12)已知F1、F2是椭圆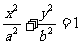 (a>b>0)的两个焦点,点P在椭圆上,且
(a>b>0)的两个焦点,点P在椭圆上,且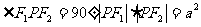 该椭圆的离心率为
该椭圆的离心率为
(A) 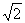 (B)
(B) 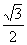 (C)
(C) 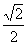 (D)
(D) 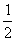
第Ⅱ卷 (非选择题共90分)
15、设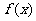 定义域为D,若满足:(1)
定义域为D,若满足:(1)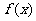 在D内是单调函数;(2)存在
在D内是单调函数;(2)存在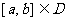 ,使
,使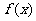 在
在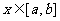 时值域也为
时值域也为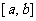 ,则称
,则称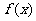 为D上的闭函数。
为D上的闭函数。
当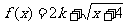 时,k的取值范围是
。
时,k的取值范围是
。
14、在棱长为a的正方体ABCD- 中,过对角线
中,过对角线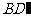 的一个平面交棱
的一个平面交棱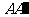 于E,交棱
于E,交棱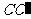 于F,则以下结论正确的是
(写出所有正确的结论序号)
于F,则以下结论正确的是
(写出所有正确的结论序号)
①四边形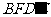 一定是平行四边形。
一定是平行四边形。
②四边形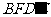 有可能是正方形。
有可能是正方形。
③四边形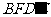 有可能是菱形。
有可能是菱形。
④四边形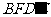 有可能垂直于平面
有可能垂直于平面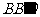
⑤四边形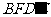 截面最小面积为
截面最小面积为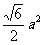 。
。
13、第一象限内有一动点Q,在过点A(3,2)且方向向量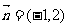 的直线
的直线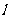 上运动,则
上运动,则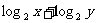 的最大值为 。
的最大值为 。
12、已知三角形两边长为1和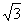 ,第三边的中线长为1,则第三边长为
。
,第三边的中线长为1,则第三边长为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com