
22.(本小题满分14分)
设数列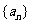 是首项为6,公差为1的等差数列;
是首项为6,公差为1的等差数列;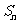 为数列
为数列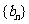 的前
的前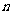 项和,且
项和,且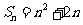
(1)求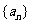 及
及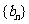 的通项公式
的通项公式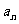 和
和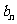 ;
;
(2)若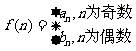 ,问是否存在
,问是否存在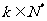 使
使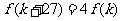 成立?若存在,求出
成立?若存在,求出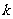 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)若对任意的正整数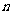 ,不等式
,不等式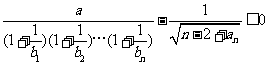 恒成立,求正数
恒成立,求正数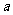 的取值范围。
的取值范围。
21.(本小题满分12分)
已知定点A(1,0)和直线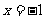 上的两个动点E,F,且
上的两个动点E,F,且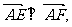 动点P满足
动点P满足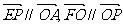 (其中O为坐标原点)
(其中O为坐标原点)
(1)求动点P的轨迹C的方程
(2)过点B(0,2)的直线l与(1)中的轨迹C相交于两个不同的点M,N,若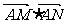 <0,求直线l的斜率的取值范围
<0,求直线l的斜率的取值范围
20.(本小题满分12分)
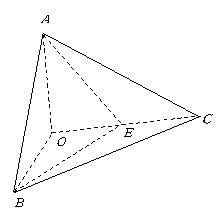
如图,已知三棱锥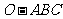 的侧棱
的侧棱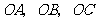 两两垂直,且
两两垂直,且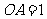 ,
,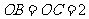 ,
,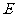 是
是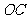 的中点.
的中点.
(1)求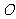 点到面
点到面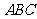 的距离;
的距离;
(2)求异面直线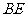 与
与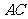 所成的角;
所成的角;
(3)求二面角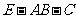 的大小.
的大小.
19.(本小题满分12分)
在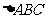 中,角
中,角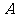 、
、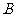 、
、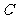 的对边分别为
的对边分别为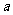 、
、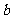 、
、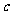 ,
,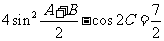 ,
,
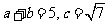 。
。
(1)求角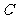 的大小; (2)求
的大小; (2)求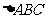 的面积。
的面积。
18.(本小题满分12分)
(理科)有A,B,C,D四个城市,它们都有一个著名的旅游点依此记为a,b,c,d把A,B,C,D和a,b,c,d分别写成左、右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分;
(1)求该爱好者得分的分布列; (2)求所得分的数学期望?
(文科)某车间准备从10名工人中选配4人到某生产线工作,为安全生产,工厂规定:一个生产线上熟练工人不得少于3人,已知这10名工人中有熟练工人8人,学徒2名。
(1)求工人配置合理的概率;
(2)为了督促安全生产,工厂安全部门每月对工人配置情况进行两次检查,求两次检查得到结果不一致的概率?
17.(本小题满分12分)
已知函数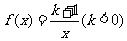 ,求使得
,求使得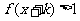 成立的
成立的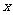 的集合
的集合
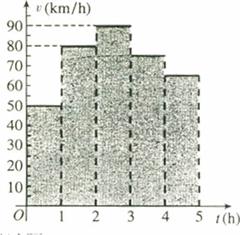
16.一辆汽车在某段路程中的行驶速度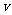 与时间
与时间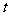 的关系如图所示,则该汽车在前3小时内行驶的路程为_________km,假设这辆汽车的里程表在汽车行驶这段路程前的读数为2006km,那么在
的关系如图所示,则该汽车在前3小时内行驶的路程为_________km,假设这辆汽车的里程表在汽车行驶这段路程前的读数为2006km,那么在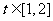 时,汽车里程表读数
时,汽车里程表读数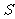 与时间
与时间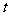 的函数解析式为__________。
的函数解析式为__________。
15. 已知
已知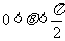 ,由不等式
,由不等式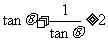 ,
,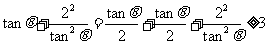 ,
,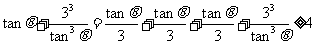 ,……,启发我们得到推广结论:
,……,启发我们得到推广结论:
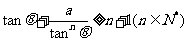 ,则
,则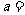 ___________。
___________。
14.已知变量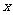 、
、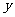 满足
满足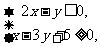 则
则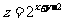 的最大值为__________。
的最大值为__________。
13.已知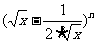 展开式中第4项为常数项,则展开式的各项的系数和为
展开式中第4项为常数项,则展开式的各项的系数和为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com