
19.(本小题满分12分)
数列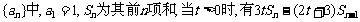 =
=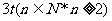
(I)求证:数列{an}是等比数列;
(II)设数列{an}的公比为f(t),作数列{bn},使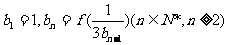 ,求数列{bn}的前n项和Bn.
,求数列{bn}的前n项和Bn.
18.(本小题满分12分)
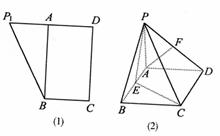
如图(1),在直角梯形P1DCB中,P1D//BC,CD⊥P1D,且P1D=8,BC=4,DC=4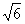 ,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置(如图(2)),使二面角P-CD-B成45°,设E、F分别是线段AB、PD的中点.
,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置(如图(2)),使二面角P-CD-B成45°,设E、F分别是线段AB、PD的中点.
(I)求证:AF//平面PEC;
(II)求平面PEC和平面PAD所成的二面角(锐角)的大小.
17.(本小题满分12分)
在△ABC中,a、b、c分别是角A、B、C的对边,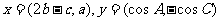 ,且x⊥y.
,且x⊥y.
(I)求角A的大小;
(II)当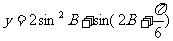 取最大值时,求角B的大小;
取最大值时,求角B的大小;
16.有下列说法:
①函数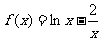 的零点所在的大致区间是(2,3);
的零点所在的大致区间是(2,3);
|
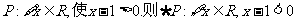
③一组数据方差越小,样本数据分布越集中、稳定;
④乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数中各抽1个,再比较大小,这种抽签方法是公平的;
⑤若函数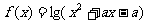 的值域是R,则a≤-4或a≥0.
的值域是R,则a≤-4或a≥0.
15.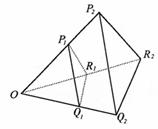 若从点O所作的两条射线OM,ON上分别有点M1,M2与点N1,N2,则三角形面积之比
若从点O所作的两条射线OM,ON上分别有点M1,M2与点N1,N2,则三角形面积之比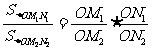 .如图,若从点O所作的不在同一平面内的三条射线OP,OQ和OR上分别有有点P1,P2,点Q1,Q2和点R1,R2,则类似的结论为
.
.如图,若从点O所作的不在同一平面内的三条射线OP,OQ和OR上分别有有点P1,P2,点Q1,Q2和点R1,R2,则类似的结论为
.
14.已知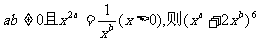 的展开式的常数项是 .
的展开式的常数项是 .
13.已知双曲线的中心在原点,一个顶点的坐标是(-3,0),且焦距与实轴长之比为5:3,则双曲线的标准方程是 .
12.设O为坐标原点,点M(2,1),点N(x,y)满足 ∠MON的最大值为 ( )
∠MON的最大值为 ( )
A.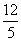 B.
B.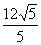 C.
C.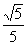 D.
D.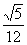
|
11.已知抛物线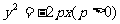 的焦点F恰好是椭圆
的焦点F恰好是椭圆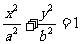 的左焦点,且两
的左焦点,且两
曲线的公共点的连线过F,则该椭圆的离心率为 ( )
A.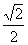 B.2(
B.2(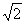 -1) C.
-1) C.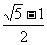 D.
D.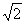 -1
-1
10.如图的阴影部分由方格纸上3个小方格组成,我们称这样的图案为L形,那么在由3×5个小方格组成的方格纸上可以画出不同位置的L形图案的个数
|
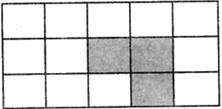
A.15 B.16 C.32 D.48
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com