
19. (本小题满分14分)
(本小题满分14分)
如图6所示,等腰△ABC的底边AB=6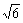 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记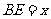 V(x)表示四棱锥P-ACFE的体积.
V(x)表示四棱锥P-ACFE的体积.
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值
18.(本小题满分14分)
在平面直角坐标系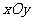 中,已知圆心在第二象限,半径为2
中,已知圆心在第二象限,半径为2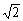 的圆C与直线
的圆C与直线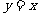 相切于坐标原点O.椭圆
相切于坐标原点O.椭圆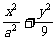 =1与圆C的一个交点到椭圆两点的距离之和为10.
=1与圆C的一个交点到椭圆两点的距离之和为10.
(1)求圆C的方程.
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆右焦点F的距离等于线段OF的长.若存在,请求出点Q的坐标;若不存在,请说明理由.
17.(本题满分12分)
下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量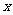 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
|
x |
3 |
4 |
5 |
6 |
|
y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=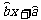 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
16.(本小题满分12分)
已知△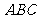 顶点的直角坐标分别为
顶点的直角坐标分别为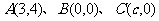 .
.
(1)若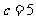 ,求sin∠
,求sin∠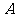 的值;
的值;
(2)若∠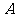 是钝角,求
是钝角,求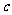 的取值范围.
的取值范围.
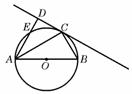
15.(几何证明选讲选做题)如图5所示,圆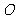 的直径
的直径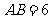 ,
,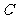 为圆周上一点,
为圆周上一点,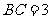 ,过
,过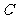 作圆的切线
作圆的切线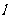 ,过
,过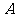 作
作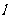 的垂线
的垂线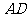 ,
,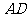 分别与直线
分别与直线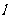 、圆交于点
、圆交于点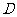 、
、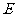 ,则∠
,则∠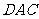 =
,线段
=
,线段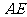 的长为 _______
图5
的长为 _______
图5
14. (不等式选讲选做题)设函数
(不等式选讲选做题)设函数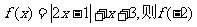 =
;若
=
;若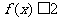 ,则
,则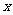 的取值范围是
.
的取值范围是
.
13.(坐标系与参数方程选做题)在平面直角坐标系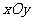 中,直线
中,直线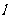 的参数方程为
的参数方程为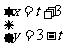 ,(参数
,(参数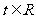 ),圆
),圆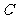 的参数方程为
的参数方程为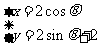 (参数
(参数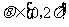 ),则圆
),则圆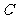 的圆心坐标为
,圆心到直线
的圆心坐标为
,圆心到直线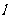 的距离为
.
的距离为
.
12.如果一个凸多面体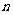 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条.这些直线中共有
棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条.这些直线中共有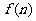 对异面直线,则
对异面直线,则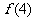 = 图4
= 图4
; 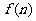 =
.(答案用数字或
=
.(答案用数字或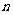 的解析式表示)
的解析式表示)
11. 在平面直角坐标系
在平面直角坐标系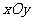 中,有一定点
中,有一定点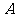 (2,1),若线段
(2,1),若线段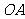 的垂直平分线过抛物线
的垂直平分线过抛物线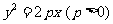 的焦点,则该抛物线的准线方程是
.
的焦点,则该抛物线的准线方程是
.
10.若向量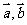 满足
满足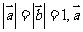 与
与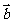 的夹角为120°,则
的夹角为120°,则 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com