
题目列表(包括答案和解析)
2.用反证法证明“如果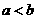 ,那么
,那么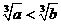 ”,假设的内容应是( )
”,假设的内容应是( )
(A)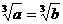 (B)
(B)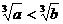
(D)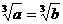 且
且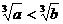 (D)
(D)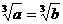 或
或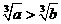
1. 对两个变量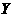 与X进行回归分析,分别选择不同的模型,它们的相关系数
与X进行回归分析,分别选择不同的模型,它们的相关系数 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
( )模型Ⅰ的相关系数
)模型Ⅰ的相关系数 为
为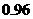 (
(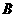 )模型Ⅱ的相关系数
)模型Ⅱ的相关系数 为
为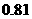
(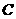 )模型Ⅲ的相关系数
)模型Ⅲ的相关系数 为
为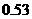 (
(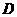 )模型Ⅳ的相关系数
)模型Ⅳ的相关系数 为
为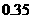
22、已知函数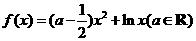 .
.
(Ⅰ)当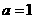 时,
时,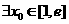 使不等式
使不等式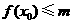 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)若在区间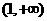 上,函数
上,函数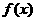 的图象恒在直线
的图象恒在直线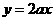 的下方,求实数
的下方,求实数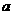 的取值范围.
的取值范围.
21、定义在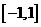 上的奇函数,已知当
上的奇函数,已知当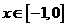 时的解析式
时的解析式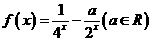
(1)
写出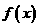 在
在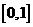 上的解析式;
上的解析式;
(2)
求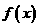 在
在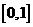 上的最大值。
上的最大值。 

20、经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t(件),价格近似满足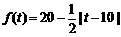 (元).
(元).
(Ⅰ)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(Ⅱ)求该种商品的日销售额y的最大值与最小值. 

19、下面(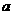 )、(
)、(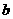 )、(
)、(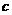 )、(
)、(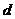 )为四个平面图。
)为四个平面图。

|
|
顶点数 |
边数 |
区域数 |
|
(a) |
4 |
6 |
3 |
|
(b) |
|
12 |
|
|
(c) |
6 |
|
|
|
(d) |
|
15 |
|
(1)数出每个平面图的顶点数、边数、区域数,
并将相应结果填入右表; 

(2)观察右表,若记一个平面图的顶点数、边数、
区域数分别为E、F、G,试推断E、F、G之
间的等量关系;
(3)现已知某个平面图有2008个顶点,且围成2008个区域,试根据以上关系确定该平面图的边数。
18、已知函数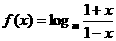 (其中
(其中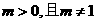 )。(1)判断函数
)。(1)判断函数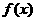 的奇偶性;(2)函数
的奇偶性;(2)函数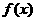 有以下性质:
有以下性质: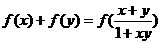 ,若
,若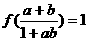 ,
,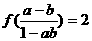 ,且
,且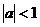 ,
,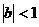 ,求
,求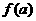 ,
,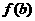 的值。
的值。 

17、某班一次期中考试之后,从全班同学中随机抽出5位,这5位同学的数学、物理分数见下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
|
数学分数x |
70 |
75 |
80 |
85 |
90 |
|
物理分数y |
73 |
77 |
80 |
88 |
86 |
先完成下面(1)-(2)的统计分析,将结果直接写在题中横线上,然后解答第(3)小题.
(1)研究变量y与x的相关关系时,计算得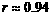 ,这说明y与x的相关程度是
.
,这说明y与x的相关程度是
.


(2)求得y与x的线性回归方程之后,该方程所表示的直线一定过点 .
(3)求y与x的线性回归方程,并估计该班本次考试数学成绩为60分的学生的物理成绩.
16、已知函数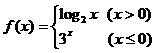 ,则
,则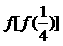 的值是
的值是
15、类比平面几何中的勾股定理:若直角三角形ABC中的两边AB、AC互相垂直,则三角形三边长满足关系: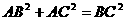 。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积满足的关系为
。
。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积满足的关系为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com