3．某科研机构为了研究中年人高血压与心脏病是否有关，随机调查了一些中年人的情况，具体数据如下表：

根据表中数据可以求得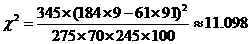，因为≥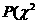

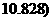
，所以有　 ▲　 的把握认为：中年人高血压与心脏病有关.

2．椭圆的参数方程是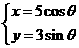 (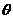为参数)，则它的离心率为　 ▲　 ．

1．极坐标系中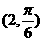，点到点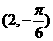的距离是　 ▲　 ．

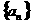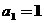22. (12分)数列满足，且，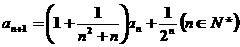

(1)　　　　　 用数学归纳法证明：.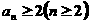 　 　　　

(2)　　　　　 已知不等式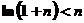对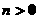成立，证明：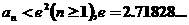

21. (12分)设。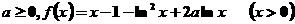

(1)令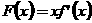，讨论内的单调性并求极值；

(2)求证：当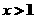时，恒有.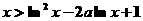 　 　　　

20.(12分)假设关于某设备的使用年限x和所支出的维修费用y(万元)，有如下的统计资料：

根据上表，通过计算机画出的散点图呈线性相关，并且已经得到：。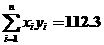

(1)　　　　 求线性回归方程；

(2)　　　　 估计使用年限为10年时，维修费用是多少？

(3)　　　　 求残差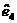的值；

(4)　　　　 求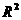，并说明模型的拟合效果. 　 　　　

　　　　　 (参考公式：)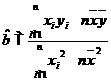

19. (12分)已知A袋中有4个白球，2个黑球；B袋中有3个白球，4个黑球。

(1)从A袋中任取2球，求取出的2球均为白球的概率；

(2)从A袋中任取1球，取出后放回，连续取三次(每次彼此独立)。设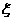为三次取球过程中取到白球的次数，求；

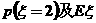(3)从A、B两个袋中各取2个球交换，求A袋中仍恰有4个白球的概率. 　 　　　

18.(12分)某工厂拟建一座平面图(如图所示)为矩形且面积为200平方米的三级污水处理池，由于地形限制，长、宽都不能超过16米，如果池外壁建造单价为每米400元，中间两条隔墙建造单价为每米248元，池底建造单价为每平方米80元(池壁的厚度忽略不计，且池无盖。)

(1)写出总造价y(元)与污水处理池长x(米)的函数关系式，并指出其定义域。

(2)求污水处理池的长和宽各为多少时，污水处理池的总造价最低？并求出最低总造价.

17. (10分)甲、乙同时参加一次面试，已知在备选的10道试题中，甲能答对其中的6道题，乙能答对其中的8道题，规定每次考试都从备选题中随机抽出3道进行测试，至少答对2道题才算通过面试。

(1)求甲能答对试题数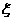的概率分布及数学期望；　 　　　

(2)求甲、乙两个至少有一个人能通过面试的概率.

16. 若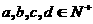，则方程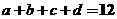共有____________组正整数解。