
题目列表(包括答案和解析)
6. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线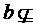 平面
平面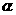 ,直线
,直线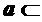 平面
平面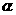 ,直线
,直线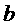 ∥平面
∥平面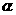 ,则直线
,则直线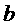 ∥直线
∥直线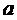 ”的结论显然是错误的,这是因为 ( )
”的结论显然是错误的,这是因为 ( )
A. 推理形式错误 B. 大前提错误 C. 小前提错误 D.非以上错误
5. 设函数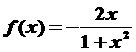 , 则
, 则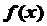 ( )
( )
A. 在(-∞,+∞)上单调递增 B. 在(-∞,+∞)上单调递减
C. 在(-1, 1 )上递增, 其余区间递减 D. 在(-1, 1 )上递减, 其余区间递增
4.下列函数中,在( 0,+∞ )上为增函数的是( )
A. y=sin2x B. y=x3-x C. y=xex D. y=ln(1+x)-x
3. 0<a<1,0<b<1,a≠b,下列各数中最大的是( )
A. 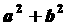 B.
B. 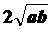 C.
C. 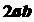 D.
D. 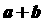
2. 化简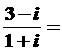 ( )
( )
A.1-2i B. 1+2i C. 2+i D. 2-i
1.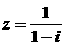 , 则
, 则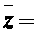 ( )
( )
A. 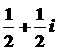 B.
B.  C.
C. 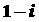 D.
D. 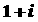
22.
已知数列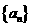 满足
满足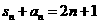 ,
,
( 1 ) 写出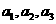 ,并推测
,并推测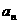 的表达式;
的表达式;
( 2 ) 用数学归纳法证明所得的结论。
(3 ) 把数列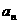 的所有数按照从小到大的
的所有数按照从小到大的
序号、左小右大的原则写成如右数表:
第k行有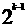 个数,第t行的第s个数
个数,第t行的第s个数
(从左数起)记为A(t,s),求通项公式A(t,s)(用t,s来表示)
21.
已知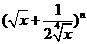 的展开式中前三项系数成等差数列。
的展开式中前三项系数成等差数列。
(1)展开式里所有的x的有理项;
(2)求展开式里系数最大的项。

20.
(1)用分析法证明: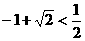
(2)用反证法证明:如果 ,那么
,那么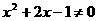 。
。
19.
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为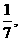 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用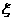 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(1)求袋中所有的白球的个数;
(2)求随机变量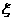 的概率分布;
的概率分布;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com