15, (满分8分) 已知抛物线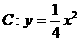

(1) 若直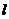线与抛物线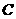相切于点,试求直线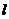的方程?　 (4分)

(2)若直线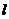过点,且与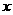轴平行,求直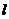线与抛物线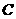所围成的封闭区域的面　

积?　　　 (4分)

16, (满分9分)

　 (1) 6个人站成一排, 其中甲、乙、两三必须相邻的排法有多少种? (3分) (作具体数字作答)

　(2) 从1、3、5、7中任选两个数, 从0、2、4、6中任选两个数, (3分)

一共可以组成多少个四位数? (用具体数字作答)

(3) 若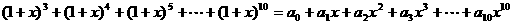,求出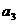的值 (算出具体数字)　 (3分)

17, 已知6件产品中, 有2件次品,现从中任取3件,试求 (9分)

　 (1) 所取出的3件产品中最多有1件次品的概率? (概率用分数表示) (3分)

　(2) 取出的3件产品中所含次品数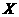的分布列? (概率用分数表示) (6分)

18, (满分9分)

　 某轮船航行过程中每小时的燃料费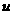与其速度的立方成正比,已知当速度为10千米/小时,燃料费10元/小时,其他与速度无关的费用每小时160元,设每千米航程成本为,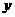

(1) 试用速度表示轮船每千米航程成本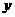　 (3分)

(2) 轮船的速度为多少时,每千米航程成本最低?　 (6分)

19, (满分9分)

　(1) 已知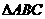的三条边分别为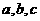, 用分析法证明: 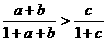(3分)

(不用分析法证明给分)

　(2) 已知数列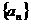的通项公式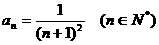,记 (6分)

,

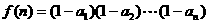①求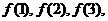并猜出的表达式. (2分)

②用数学归纳法证明你的猜想. (4分)

13、 　　　 　　　　　 ；　　 14、　 　　 　　　　　　　　；

11、　 　　　　　 　　；　　 12、　 　　　　　　　 　　 ；

15, (满分8分)某医院有内科医生6名，外科医生4名，现要选派5名参加赈灾医　

疗队。

(1)某内科医生必须参加，某外科医生不能参加，有多少种？(4分)

(2)至少有一名内科医生和至少有一名外科医生参加有多少种选？(4分)

16, (满分9分)

一盒中放有除颜色不同外，其余完全相同的黑球和白球，其中黑球2个，白球3个。

(1)从盒中同时摸出两个球，求两球颜色恰好相同的概率；(4分)

(2)从盒中摸出一个球，放回后再摸出一个球，求两球颜色恰好不同的概率 (5分)

17, (满分9分)　 数列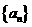满足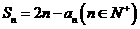

(1)计算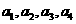，并由此猜想通项公式；(4分)

(2)用数学归纳法证明①中的猜想。(5分)

18, (满分9分) 已知tana，tanb是关于x的一元二次方程x²+px+2=0的两实根.

(1)求证：；(4分)(2)求证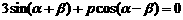：. (5分)

　 (要求用综合法)　　　　　　　　　　　 (要求用分析法)

19, (满分9分)已知函数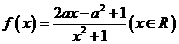，其中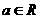

(1)当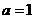时，求曲线在点处的切线方程；(3分)

(2)当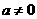时，求函数的单调区间与极大值。(6分)

21、(14分)

已知直三棱柱ABC-A₁B₁C₁的底面边长为6，D是BC边上的中点，E点满足。

(1)在怎样的条件下，平面ACE⊥平面AC₁D？

(2)在(1)的条件下，求直线A₁B₁与平面ACE所成的角的正弦值。

(3)在(1)的条件下求点A₁到平面AC₁D的距离。

20、(13分)已知正四棱柱ABCD-A₁B₁C₁D₁中，AB=2，　 AA₁=4， E为BC中点，F为直线CC₁上的动点，设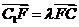

(1)当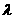为何值时，BD₁⊥EF？

(2)当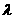=1时，求二面角F-DE-C的大小　　　　　　　　　　　　　　　

19、(12分)已知△ABC边长为2的等边三角形，PC⊥平面ABC，PC=2，D是AP上一动点。

(1)D在运动过程中，是否有可能使AP⊥面BCD？请说明理由

(2)若D是AP的中点，求直线BD与面PBC所成的角？

18、(12分)正四棱柱ABCD-A₁B₁C₁D₁中AA₁=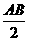=1，点E、M分别为A₁B，CC₁的中点，过点A₁、B、M三点的平面A₁BMN交C₁D₁于点N

(1)求证：EM∥平面A₁B₁C₁D₁

(2)求两异面直线EM与C₁D₁的距离

17、(12分)

(1)从长度为1、2、3、4、5的五条线段中，任取三条的不同取法共有n种，在这些取法中，以取出的三条线段为边可组成钝角三角形的个数为m。求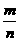

(2)设(2x+1)⁴=a₀+a₁x+a₂x²+a₃x³+a₄x⁴求(a₀+a₂+a₄)·(a₁+a₃)

16、(12分)已知直三棱柱ABC-A₁B₁C₁中，AC=BC=AA₁=a，AC⊥BC E、F分别为AB、BC的中点，G为AA₁上一点，且AC₁⊥EG

(1)试确定G的位置

(2)求异面直线AC₁与FG所成的角