
题目列表(包括答案和解析)
5.
(1988)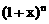 的展开式中,若第三项与第六项的系数相等,则
的展开式中,若第三项与第六项的系数相等,则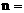 _____。[7]
_____。[7]
4.
(1987)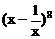 的展开式中,
的展开式中,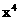 的系数与
的系数与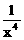 的系数之差是_________。[0]
的系数之差是_________。[0]
3.
(1986)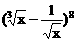 的展开式中,x的一次项的系数是___________。[28]
的展开式中,x的一次项的系数是___________。[28]
2.
(1985文)求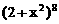 的展开式中
的展开式中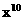 的系数。[448]
的系数。[448]
1.
(1985理)求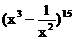 的展开式中的常数项。[-5005]
的展开式中的常数项。[-5005]
22.(本小题满分14分)
已知A(4,0)、N(1,0),曲线C上的任意一点P满足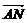 、
、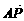 =6|
=6|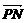 |,
|,
(1)求点P的轨迹方程;
(2)求|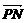 |的取值范围;
|的取值范围;
(3)若M(-1,0),求∠MPN的取值范围.
解:(1)设P(x,y),则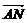 =(-3,0),
=(-3,0),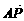 =(x-4,y),
=(x-4,y),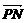 =(1-x,y).
=(1-x,y).
∵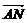 ·
·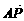 =6|
=6|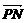 |,
|,
∴-3(x-4)+0·y=6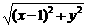 ,
,
化简得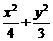 =1. 4分
=1. 4分
(2)由(1)得|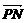 |=
|=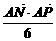 =-
=- (x-4).
(x-4).
又-2≤x≤2,
∴|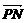 |的取值范围为[1,3]. 8分
|的取值范围为[1,3]. 8分
(3)设|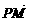 |=m,|
|=m,|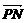 |=n,
|=n,
∵M、N正好是椭圆的两个焦点,
∴cos∠MPN=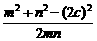
=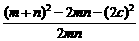 =
=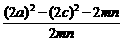
=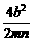 -1=
-1=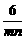 -1≥
-1≥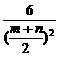 -1=
-1=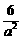 -1=
-1= .
.
又∠MPN∈(0,π),
∴∠MPN的取值范围是[0,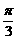 ]. 14分
]. 14分
21.(本小题满分12分)
已知正数项数列{an}和{bn}满足bn= +
+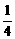 an,bn+1=bn(1-
an,bn+1=bn(1-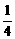 an+12)(n∈N*),a1=1.
an+12)(n∈N*),a1=1.
(1)求数列{an}和{bn}的前4项;
(2)求数列{an}和{bn}的通项公式.
解:(1)∵
对一切n∈N*都成立,
又a1=1,∴b1= +
+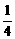 a1=
a1=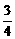 .
.
由①②③式得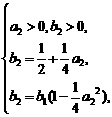
解得a2=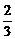 ,b2=
,b2=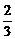 ,
,
同理解得a3= ,b3=
,b3=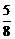 和a4=
和a4=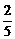 ,b4=
,b4=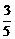 ,
,
∴数列{an}的前4项为a1=1,a2=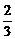 ,a3=
,a3= ,a4=
,a4=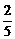 ,数列{bn}的前4项为b1=
,数列{bn}的前4项为b1=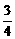 ,b2=
,b2=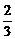 ,b3=
,b3=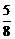 ,b4=
,b4=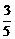 . 6分
. 6分
(2)由a1=1=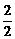 ,a2=
,a2=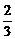 ,a3=
,a3= =
=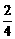 ,a4=
,a4=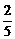 猜想数列{an}的通项公式为an=
猜想数列{an}的通项公式为an=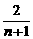 (n∈N*).④
(n∈N*).④
数学归纳法证明如下:
当n=1、2、3、4时,由前计算知公式④成立.
设n=k(k≥4)时,公式④成立,即ak=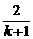 .
.
当n=k+1时,由①②③式得
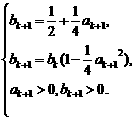
消去bk+1得
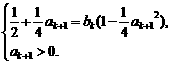 ⑤
⑤
又bk= +
+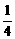 ak=
ak= +
+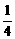 ×
×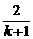 =
=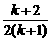 ,把它代入⑤式解得
,把它代入⑤式解得
ak+1=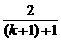 ,
,
即n=k+1时,公式④也成立.
∴对一切n∈N*,an=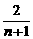 成立,此时bn=
成立,此时bn= +
+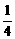 an=
an= +
+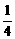 ×
×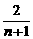 =
=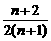 .
.
∴数列{an},{bn}的通项公式分别为
an=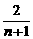 ,bn=
,bn=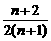 . 12分
. 12分
说明:可先猜想数列{bn}的通项公式,再用数学归纳法证明,最后由②式解得{an}的通项公式.
20.(本小题满分12分)
已知函数f(x)=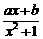 在x=2处有一个极大值.
在x=2处有一个极大值.
(1)求a、b的关系式,并判断a的符号;
(2)求f(x)的单调区间.
解:(1)f′(x)=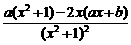 =
=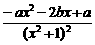 . ①
. ①
∵f(x)在x=2处有一个极大值,
∴f′(2)=0,从而3a+4b=0. ②
将b=-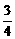 a代入①得
a代入①得
f′(x)=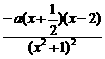 .
.
∵f(x)在x=2处有极大值,
∴当- <x<2时,f′(x)>0;x>2时,
<x<2时,f′(x)>0;x>2时,
f′(x)<0,∴a>0. 6分
(2)令f′(x)>0解得- <x<2,从而f(x)在(-
<x<2,从而f(x)在(- ,2)内是增函数;
,2)内是增函数;
令f′(x)<0,解得x<- 或x>2,从而f(x)在(-∞,-
或x>2,从而f(x)在(-∞,- )或(2,+∞)内是减函数.12分
)或(2,+∞)内是减函数.12分
19.(本小题满分12分)
二人掷一颗骰子,两人各掷一次,点数大者为胜,但这个骰子可能不太规则,以致k点出现的概率是Pk(k=1,2,3,4,5,6).在这种情况下,
(1)求二人平局的概率P.
(2)证明P≥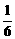 ;并证明如果P=
;并证明如果P=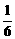 ,则Pk=
,则Pk=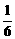 (k=1,2,3,4,5,6).
(k=1,2,3,4,5,6).
(1)解:P=P12+P22+…+P62. 4分
(2)证明:∵P1+P2+…+P6=1,
(P1-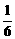 )2+(P2-
)2+(P2-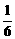 )2+…+(P6-
)2+…+(P6-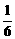 )2
)2
=P12+P22+…+P62-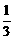 (P1+P2+…+P6)+
(P1+P2+…+P6)+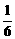
=P-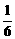 ≥0,
≥0,
∴P≥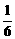 ,当P=
,当P=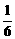 时,P1=P2=…=P6=
时,P1=P2=…=P6=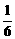 . 12分
. 12分
18.(本小题满分12分)
已知正四棱柱ABCD-A′B′C′D′的底面边长为3,高为4.
(1)平面ABCD内是否存在与AB不平行的直线与BC′垂直?证明你的结论.
(2)求二面角A′-BC′-B′的大小.
(3)求点D′到平面A′BC′的距离.
解法一:(几何法)(1)不存在.
证明:假设平面ABCD内存在与AB不平行的直线l与BC′垂直.
∵ABCD-A′B′C′D′是正四棱柱,
∴AB⊥BC′.
又AB与l相交,
∴BC′⊥平面ABCD.
又BB′⊥平面ABCD,这与“过一点只能作一条直线与一个平面垂直”相矛盾.故平面ABCD内不存在与AB不平行的直线l与BC′垂直. 4分
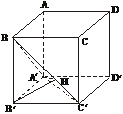
(2)作BH⊥BC′于H.
连结A′H.
∵A′B′⊥平面BB′C′,
∴A′H⊥BC′.
∴∠A′HB′为二面角A′-BC′-B′的平面角.
易求得B′H=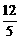 ,
,
A′H=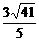 .
.
又A′B′=3,
∴△A′B′H中,cos∠A′HB′=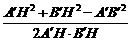 =
=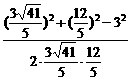 =
=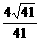 .
.
∴∠A′HB′=arccos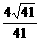 为所求. 8分
为所求. 8分
(3)设d为所求距离.
∵VD′-A′BC′=VB-A′C′D′,
∴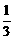 S△A′BC′·d=
S△A′BC′·d=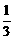 S△A′C′D′·BB′
S△A′C′D′·BB′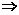
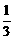 ·
·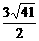 ·d=
·d=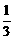 ·(
·( ·32)·4
·32)·4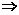 d=
d=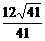 为所求. 12分
为所求. 12分
解法二:(向量法)(1)不存在.
证明:建立如图空间直角坐标系.不妨假设平面ABCD内存在直线BE(E在AD上且与A不重合)与BC′垂直(如图).
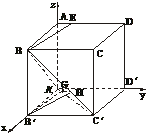
设E(0,t,4)(t≠0),
则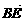 =(0,t,4)-(3,0,4)=(-3,t,0).
=(0,t,4)-(3,0,4)=(-3,t,0).
又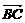 =
=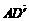 =
=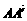 +
+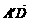 =(0,0,-4)+(0,3,0)=(0,3,-4),
=(0,0,-4)+(0,3,0)=(0,3,-4),
∴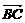 ·
·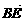 =(0,3,-4)·(-3,t,0)=3t=0
=(0,3,-4)·(-3,t,0)=3t=0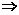 t=0,这与t≠0矛盾.
t=0,这与t≠0矛盾.
∴平面ABCD内不存在与AB不平行的直线l与BC′垂直.
(2)如图,作A′H⊥BC′于H,连结B′H.
∵A′B′⊥平面BB′C′,
∴B′H是A′H在平面BB′C′内的射影.
∴B′H⊥BC′.
∴∠A′HB′就是二面角A′-BC′-B′的平面角.
设H(3,y,z),∵B′(3,0,0),
∴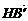 =(0,-y,-z).
=(0,-y,-z).
又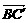 =(3,3,0)-(3,0,4)=(0,3,-4),
=(3,3,0)-(3,0,4)=(0,3,-4),
∴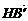 ·
·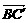 =-3y+4z.
=-3y+4z.
∵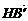 ⊥
⊥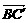 ,∴-3y+4z=0. ①
,∴-3y+4z=0. ①
又由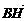 =λ
=λ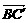 ,可得4y+3z-12=0. ②
,可得4y+3z-12=0. ②
解①②联立的方程组,得y=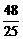 ,z=
,z=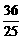 .
.
故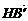 =(3,0,0)-(0,
=(3,0,0)-(0,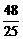 ,
,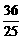 )=(3,-
)=(3,-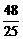 ,-
,-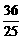 ),
),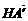 =(-3,-
=(-3,-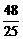 ,-
,-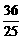 ).
).
又易得|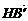 |=
|=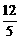 ,|
,|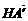 |=
|=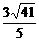 .
.
∴cos∠A′HB′=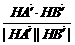
=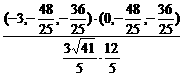
=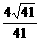 .
.
∴∠A′HB′=arccos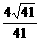 为所求. 8分
为所求. 8分
(3)由(2)可知BC′⊥平面A′HB′.
∵BC′ 平面A′BC′,
平面A′BC′,
∴平面A′HB′⊥平面A′BC′.
作B′G⊥A′H于G,则B′G⊥平面A′BC′,B′G就是点B′到平面A′BC′的距离.
∴B′G=B′H·sin∠A′HB′=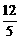 ·
·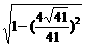 =
=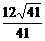 .
.
∵ABCD-A′B′C′D′是正四棱柱,
∴易证点D′与点B′到平面A′BC′的距离相等.
∴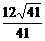 为所求. 12分
为所求. 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com