
题目列表(包括答案和解析)
2. 已知角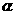 的终边经过点
的终边经过点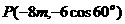 ,且
,且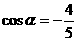 ,则
,则 的值是( )
的值是( )
A、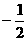 B、
B、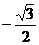 C、
C、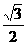 D、
D、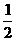
1. 已知集合A={x|0≤x≤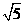 ,x∈Z},集合B={x|x=2a,a∈A},则集合A∩B等于 ( )
,x∈Z},集合B={x|x=2a,a∈A},则集合A∩B等于 ( )
A.{0,2} B.{0,1} C.{1,2} D.{0}
22.(本小题满分14分)
已知二次函数f(x)=ax2+(a+1)x-a,方程f(x)=0两实根的差的绝对值等于2.
(Ⅰ)求实数a的值.
(Ⅱ)是否存在实数p、q,使得函数F(x)=pf[f(x)]+q f(x),在区间(-∞,-3)内是增函数,在区间(-3,0)内是减函数?若存在,求p、q所要满足的条件;若不存在,说明理由.
福州市2003-2004学年第二学期高三质量检查
21.(本小题满分12分)
设双曲线C1的方程为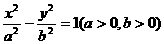 ,A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
,A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
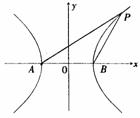 (Ⅰ)求Q点的轨迹方程;
(Ⅰ)求Q点的轨迹方程;
(Ⅱ)设(I)中所求轨迹为C2,C1、C2
的离心率分别为e1、e2,当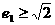 时,e2的取值范围.
时,e2的取值范围.
20.(本小题满分12分)
已知数列{an}中,a2=a+2(a为常数);Sn是{an}的前n项和,且Sn是nan与na的等差中项.
(Ⅰ)求a1, a3 ;
(Ⅱ)猜想an的表达式,并用数学归纳法加以证明;
(Ⅲ)求证以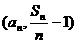 为坐标的点Pn(n=1, 2, …)都落在同一直线上.
为坐标的点Pn(n=1, 2, …)都落在同一直线上.
19.(本小题满分12分)
冰箱中放有甲、乙两种饮料各5瓶,每次饮用时从中任意取1瓶甲种或乙种饮料,取用甲种或乙种饮料的概率相等.
(Ⅰ)求甲种饮料饮用完毕而乙种饮料还剩下3瓶的概率;
(Ⅱ)求甲种饮料被饮用瓶数比乙种饮料被饮用瓶数至少多4瓶的概率.
18.(本小题满分12分)
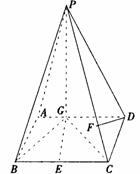 已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=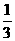 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为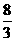 .
.
(Ⅰ)求异面直线GE与PC所成的角;
(Ⅱ)求点D到平面PBG的距离;
(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求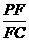 的值.
的值.
17.(本小题满分12分)
已知函数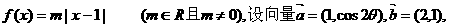
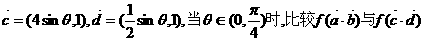 的大小.
的大小.
16.设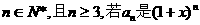 展开式中含x2项的系数,则
展开式中含x2项的系数,则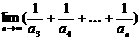 =
=
.
15.已知P是椭圆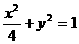 上的一点,F1、F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是
.
上的一点,F1、F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com