
题目列表(包括答案和解析)
2.等差数列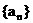 前四项和为40, 末四项和为72, 所有项和为140, 则该数列共有 ( )
前四项和为40, 末四项和为72, 所有项和为140, 则该数列共有 ( )
A.9项 B.12项 C.10项 D.13项
1.设全集U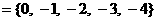 , 集合M
, 集合M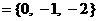 , N
, N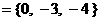 , 那么
, 那么
(CUM)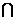 N为 ( )
N为 ( )
A.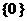 B.
B.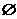 C.
C.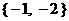 D.
D.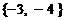
22.(本题满分14分)对于函数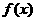 ,若存在
,若存在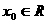 ,使
,使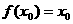 成立,则称点
成立,则称点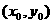 为函数的不动点。(1)已知函数
为函数的不动点。(1)已知函数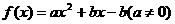 有不动点(1,1)和(-3,-3)求
有不动点(1,1)和(-3,-3)求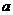 与
与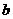 的值;(2)若对于任意实数
的值;(2)若对于任意实数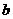 ,函数
,函数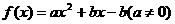 总有两个相异的不动点,求
总有两个相异的不动点,求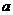 的取值范围;(3)若定义在实数集R上的奇函数
的取值范围;(3)若定义在实数集R上的奇函数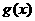 存在(有限的)
存在(有限的)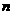 个不动点,求证:
个不动点,求证: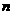 必为奇数。
必为奇数。
21.(本小题满分12分)设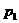 ,
,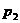 分别是直线
分别是直线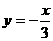 和
和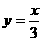 上的动点,(
上的动点,(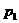 ,
,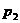 两点的纵坐标符号相同),O是坐标原点,且△
两点的纵坐标符号相同),O是坐标原点,且△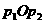 的面积为9。①求线段
的面积为9。①求线段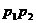 的最小值;②求线段
的最小值;②求线段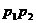 的中点M的轨迹方程;③设点
的中点M的轨迹方程;③设点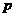 是直线
是直线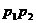 上的点,且点
上的点,且点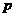 分有向线段
分有向线段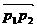 所成的比是
所成的比是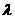 (
(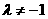 ),求点
),求点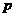 的轨迹方程。
的轨迹方程。
20.(本小题12分)学校餐厅每天供应1000名学生用餐,每星期一有A、B两样特色菜可供选择(每个学生都将从二者中选一),调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A 、B
、B 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)试以A 表示A
表示A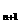 ;(2)若A
;(2)若A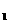 =200,求{A
=200,求{A }的通项公式;
}的通项公式;
(3)问第n个星期一时,选A与选B的人数相等?
19.(本题满分12分)已知向量 a=(1,1),b=(1,0),c满足a c=0且|a|=|b|,b
c=0且|a|=|b|,b c>0.
c>0.
1).求向量c;2)若映射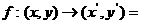
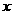 a+
a+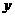 c,
c,
①求映射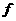 下(1,2)的原象;
下(1,2)的原象;
②若将(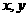 )看作点的坐标,问是否存在直线
)看作点的坐标,问是否存在直线 使得直线上的任一点在映射
使得直线上的任一点在映射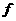 的作用下点仍在直线上,若存在求出直线
的作用下点仍在直线上,若存在求出直线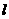 的方程,否则说明理由。
的方程,否则说明理由。
18.(本小题12分) 已知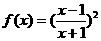
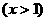 ,(1)若
,(1)若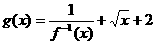 ,求
,求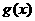 的最小值;(2)若不等式
的最小值;(2)若不等式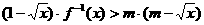 对于一切
对于一切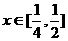 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
17. (本题满分12分)已知集合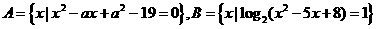 ,集合
,集合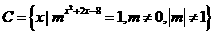 满足
满足 ,求实数
,求实数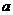 的值。
的值。
16.在等比数列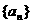 中,若
中,若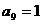 ,则有等式
,则有等式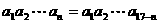 ,
,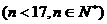 。类比上述性质,相应的在等差数列
。类比上述性质,相应的在等差数列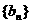 中,若
中,若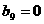 ,则有等式
成立。
,则有等式
成立。
15.已知函数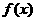 满足:
满足: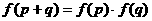 ,
,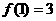 ,则
,则
 +
+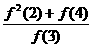 +
+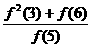 +
+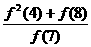 +
+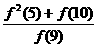 = 。
= 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com