
题目列表(包括答案和解析)
4.函数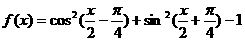 是 ( )
是 ( )
A.周期为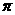 的奇函数
B. 周期为
的奇函数
B. 周期为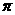 的偶函数
的偶函数
C.周期为2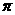 的奇函数
D。周期为2
的奇函数
D。周期为2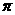 的偶函数
的偶函数
3.命题甲: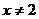 或
或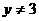 ;命题乙:
;命题乙: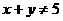 ,则
( )
,则
( )
A.甲是乙的充分非必要条件; B.甲是乙的必要非充分条件;
C. 甲是乙的充要条件; D.甲既不是乙的充分条件,也不是乙的必要条件.
2. 设a>b>c,且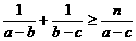 ,则n的最大值为
( )
,则n的最大值为
( )
A.2 B.3 C.4 D.5
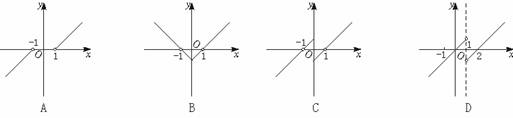
1.奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则函数f(x-1)的图象为( )
20.(13分)如图,把正△ABC分成有限个全等的小正三角形,且在每个小三角形的顶点上都放置一个非零实数,使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等。设点A为第1行,…,BC为第n行,记点A上的数为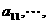 第i行中左起第j个数为
第i行中左起第j个数为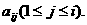 若
若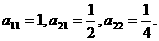
(1)求 ;
;
(2)试归纳出 的表达式(用含n,m的式子表示,不必证明);
的表达式(用含n,m的式子表示,不必证明);
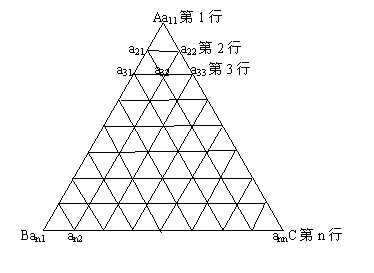 (3)记
(3)记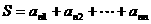 ,证明
,证明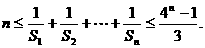
北京师大附中2005--2006学年度上学期高三数学
19.(理科做)已知函数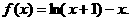
(1)求函数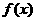 的单调区间;
的单调区间;
(2)若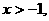 证明:
证明: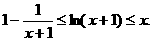
(文科做)已知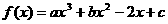 在
在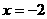 时有极大值6,在
时有极大值6,在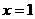 时有极小值,求
时有极小值,求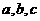 的值;并求
的值;并求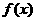 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.
18.((理科做)某同学参加法律知识竞赛,共有4道试题,他答对每道题的概率都是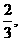 且回答各题相互独立. 竞赛规定: 参赛者未答题前有底分300分,每答对一题得100分,答错扣100分,一开始即连答错3道题就失去资格自动下场.
且回答各题相互独立. 竞赛规定: 参赛者未答题前有底分300分,每答对一题得100分,答错扣100分,一开始即连答错3道题就失去资格自动下场.
(1 ) 求此同学答题数目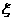 的分布列和数学期望;
的分布列和数学期望;
(2 ) 求此同学最后得分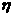 的分布列和数学期望;
的分布列和数学期望;
(3 ) 若另有5名同学都与此名同学水平相当,求他们6人中到最后能留在场上的人数 的期望和方差.
的期望和方差.
(文科做) 在一次招聘面试中,备有10道题,甲能答对其中的6道题,乙能答对其中的8道题,规定每人分别从10道题中随机抽取3道题测试(答完放回),若至少答对2道题者合格.
(1 ) 求甲乙两人至少有一人测试合格的概率;
(2 ) 求甲乙两人中恰有一人测试合格的概率.
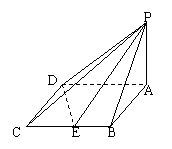
17.如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD = 60°,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为45°.
(1 ) 求点A到平面PDE的距离;
(2 ) 在PA上确定一点F,使BF∥平面PDE;
(3 ) 求异面直线PC与DE所成的角(用反三角函数表示);
(4 ) 求面PDE与面PAB所成的不大于直二面角的二面角的大小(用反三角函数表示).
16.已知向量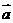 =
=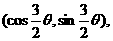
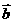 =
=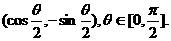
(1)求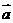 ·
·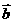 及|
及|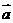 +
+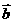 |;
|;
(2 ) 若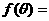
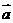 ·
·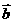
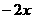 |
|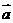 +
+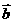 |的最小值为
|的最小值为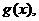 求
求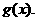
15.已知关于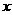 的不等式
的不等式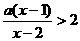 的解集为A,且
的解集为A,且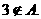
(1)求实数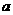 的取值范围;
的取值范围;
(2)求集合A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com