20.(12分)已知a=(cosθ，sinθ)，b=(cosβ，sinβ)，a与b之间有关系式|ka+b|=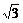|a－kb|(k＞0).

(1)用k表示a·b；

(2)求a·b的最小值，并求此时a与b夹角的大小.

解：(1)将|ka+b|=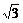|a－kb|两边平方得a·b==.

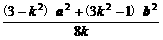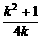(2)∵(k－1)²≥0，

又k＞0，∴≥=，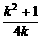

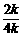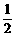即a·b≥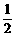，cosα=.

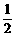又0°≤α≤180°，故a与b的夹角为60°.

19.(12分)△ABC的三个内角A、B、C满足下列条件：

①A＜B＜C；②A、B、C成等差数列；③tanA·tanC=2+.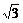

(1)求A、B、C的大小；

(2)若AB边上的高为4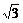，求a、b、c的大小.

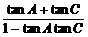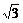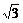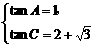解：(1)由题意知B=60°，A+C=120°，tan(A+C)==－tanB=－，∴tanA+tanC=3+.故或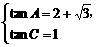(舍)，故A=45°，B=60°，C=75°.

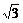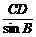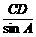(2)过C作CD⊥AB于点D，则CD＝4，在Rt△ACD和Rt△ABC中，由正弦定理得a==8，b==4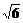，c=AD+DB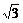=4+4.

18.(12分)向量a=(1，cos2θ)，b=(2，1)，c=(4sinθ，1)，d=(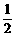sinθ，1)，其中θ∈(0，).

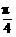(1)求a·b－c·d的取值范围；

(2)若函数f(x)=|x－1|，判断f(a·b)与f(c·d)的大小，并说明理由.

解：(1)a·b=2+cos2θ，c·d=2sin²θ+1=2－cos2θ.

∵a·b－c·d=2cos2θ，

∴0＜θ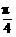＜.∴0＜2θ＜.

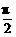∴0＜cos2θ＜1.∴0＜2cos2θ＜2.

∴a·b－c·d的取值范围是(0，2).

(2)f(a·b)=|2+cos2θ－1|=|1+cos2θ|=2cos²θ，

f(c·d)=|2－cos2θ－1|=|1－cos2θ|=2sin²θ.

于是有f(a·b)－f(c·d)=2(cos²θ－sin²θ)=2cos2θ.

∵0＜θ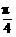＜，∴0＜2θ＜.

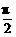∴2cos2θ＞0.∴f(a·b)＞f(c·d).

17.(12分)已知向量a=(3，－4)，求：

(1)与a平行的单位向量b；

(2)与a垂直的单位向量c；

(3)将a绕原点逆时针方向旋转45°得到的向量e的坐标.

解：(1)设b=λa，则|b|=1，b=(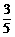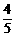，－)或b=(－，).

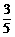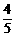(2)由a⊥c，a=(3，－4)，可设c=λ(4，3)，求得c=(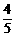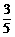，)或c=(－，－).

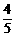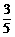(3)设e=(x，y)，则x²+y²=25.

又a·e=3x－4y=|a||e|cos45°，即3x－4y=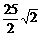，由上面关系求得e=(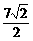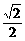，－)，或e=(－，－)，

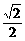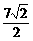而向量e由a绕原点逆时针方向旋转45°得到，故e=(，－).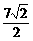

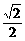16.已知直线l₁过点(0，t)，方向向量为(1，1)，直线l₂过点(t，1)，方向向量为(1，－2)，P为l₁、l₂的交点，当t变化时，P的轨迹方程为____________.

解析：l₁方程为x－y+t=0，l₂方程为2x+y－1－2t=0，两式消去t即得P的轨迹方程.

答案：4x－y－1=0

15.在△ABC中，记BC=a，AC=b，AB=c，若9a²+9b²－19c²=0，则=____________.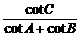

解析：=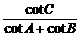

===

=

==.

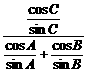
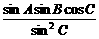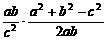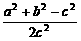
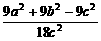
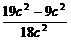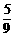答案：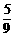

14.已知向量a=(1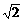，)，b=(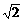－，1)，若正数k和t满足x=a+(t²+1)b与y=－ka+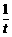b垂直，则k的最小值是____________.

解析：x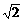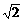=(1－－t²，1+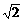+t²)，y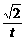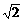=(－k－，－k+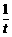)，由x⊥y得x·y=0.又t＞0，∴k=t+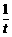≥2.∴当t=1时，k的最小值为2.

答案：2

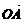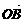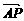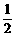
13. =3e₁，=3e₂，且=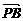，则=____________.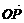

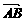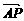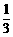
解析：=3e₂－3e₁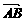，==e₂－e₁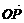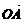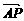，=+=2e₁+e₂.

答案：2e₁+e₂

12.在平面直角坐标系中，O为原点，OA=a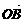，=b，对任意一点M，它关于A的对称点为S，S关于点B的对称点为N，则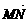用a、b表示为

A.2(b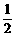－a)　　　　　　　　　　　　　　　　　　　　　　　　　 B.(a－b)

C.a+b　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.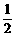(a+b)

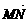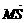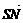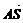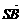解析：=+=2+2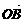=2－2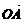.(四边形OASB是平行四边形)

答案：A

11.命题p：|a|=|b|且a∥b；命题q：a=b，则p是q的

A.充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　 B.必要不充分要件

C.充分必要条件　　　　　　　　　　　　　　　　　　　　　　　 D.既不充分又不必要条件

解析：当a∥b且a与b方向相反时，即使|a|=|b|，也不能得到a=b，故|a|=|b|且a∥b不是a=b的充分条件，而是必要不充分条件.

答案：B