
题目列表(包括答案和解析)
17.(本小题满分12分)
已知函数f(x)=cos4x-2sinxcosx-sin4x.
(1)求f(x)的最小正周期;
(2)若x∈[0,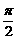 ],求f(x)的最大值、最小值.
],求f(x)的最大值、最小值.
解:(1)因为f(x)=cos4x-2sinxcosx-sin4x=(cos2x+sin2x)·(cos2x-sin2x)-sin2x=cos2x-sin2x=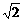 cos(2x+
cos(2x+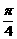 ),
),
所以f(x)的最小正周期T=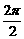 =π. 6分
=π. 6分
(2)因为0≤x≤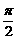 ,所以
,所以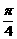 ≤2x+
≤2x+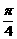 ≤
≤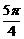 .
.
当2x+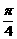 =
=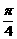 时,cos(2x+
时,cos(2x+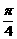 )取得最大值
)取得最大值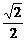 ;
;
当2x+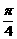 =π时,cos(2x+
=π时,cos(2x+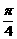 )取得最小值-1.
)取得最小值-1.
所以f(x)在[0,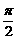 ]上的最大值为1,最小值为-
]上的最大值为1,最小值为-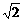 . 12分
. 12分
16.关于正四棱锥P-ABCD,给出下列命题:
①异面直线PA与BD所成的角为直角;
②侧面为锐角三角形;
③侧面与底面所成的二面角大于侧棱与底面所成的角;
④相邻两侧面所成的二面角为钝角.
其中正确命题的序号是___________.
解析:
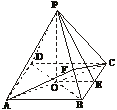
①对,如图,顶点P在底面上的射影为底面中心O.
∵AC⊥BD,
∴PA⊥BD,即PA与BD所成的角为直角.
②对,设正四棱锥底面边长为a,侧棱长为b,
则AC=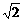 a,OA=OB=
a,OA=OB=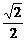 a.
a.
∵b>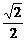 a,在△PAB中,PA2+PB2-AB2=2b2-a2>2(
a,在△PAB中,PA2+PB2-AB2=2b2-a2>2(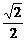 a)2-a2=0,
a)2-a2=0,
∴∠APB为锐角,故△APB为锐角三角形,即侧面为锐角三角形.
③对,取BC中点E,连PE、OE,易知∠PEO为侧面与底面所成的角,∠PBO为侧棱与底面所成的角,sin∠PEO=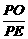 ,sin∠PBO=
,sin∠PBO=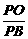 .
.
∵PB>PE,
∴sin∠PEO>sin∠PBO.
∴∠PEO>∠PBO.
④对,作AF⊥PB于F,连FC,易证FC⊥PB,
∴∠AFC为相邻两侧面所成的二面角.
∵AF<AB,CF<BC,在△AFC中,AF2+CF2-AC2<AB2+BC2-AC2=0,从而∠AFC>90°.
故相邻两侧面所成的二面角为钝角.
答案: ①②③④
15.四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有_______种.
解析:
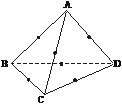
从10个点中任取4个的组合数为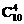 =210种.
=210种.
其中4点共面的分三类.
(1)4点在同一侧面或底面的共4组,即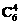 ×4=60种.
×4=60种.
(2)每条棱的中点与它的对棱上三点共面,这样的共6种.
(3)在6个中点中,4点共面数有3种.
故4点不共面的取法有210-(60+6+3)=141种.
答案: 141
14.如下图的电路中有a、b、c三个开关,每个开关断开或闭合的概率都是 ,且是相互独立的,则在某时刻灯泡甲、乙亮的概率分别是_______.
,且是相互独立的,则在某时刻灯泡甲、乙亮的概率分别是_______.
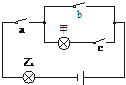
解析: 甲亮须a、c闭合,b开启,
∴P甲= ×
× ×
× =
=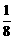 .
.
乙亮a必须闭合,b、c只需一个闭合即可,
∴P乙= ×(
×( ×
× +
+ ×
× +
+ ×
× )=
)=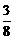 .
.
答案: 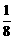 ,
,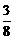
13.在(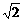 +
+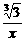 )2004的展开式中,系数为有理数的项共有_______项.
)2004的展开式中,系数为有理数的项共有_______项.
解析: 易知Tr+1=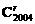 21002-
21002-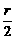 ·
·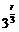 x-r.其系数为有理数的充要条件是r为2与3的倍数,即r被6整除,所以r=6k(k∈Z).
x-r.其系数为有理数的充要条件是r为2与3的倍数,即r被6整除,所以r=6k(k∈Z).
∵0≤6k≤2004,
∴0≤k≤334(k∈Z).
∴k=0,1,2,…,334.
系数为有理数的项共有335项.
或利用等差数列通项公式,由2004=6(n-1),解得n=335.
答案: 335
12.已知f(x)=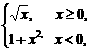 则f′(1)、f′(-1)等于
则f′(1)、f′(-1)等于
A.-2 B.-3 C.-1 D.1
解析: f′(x)=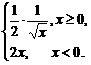
∴f′(1)·f′(-1)=-1.
答案: C
普通高等学校招生全国统一考试仿真试卷
数 学 理工农医类(四)
第Ⅱ卷 (非选择题 共90分)
11.若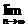 (a·
(a·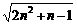 -nb)=1,则ab的值是
-nb)=1,则ab的值是
A.8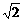 B.4
B.4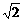 C.8 D.16
C.8 D.16
解析: 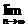 (a·
(a·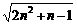 -nb)=
-nb)=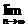
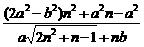 存在,
存在,
则2a2-b2=0. ①
∴原式=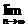
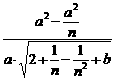 =1.
=1.
∴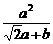 =1. ②
=1. ②
由①②可知,a=2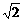 ,b=4.
,b=4.
∴ab=8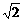 .
.
答案: A
10.一名射击运动员命中的概率为0.7,那么他射击21次后最可能的命中次数是
A.13或14 B.14或15 C.16或17 D.17或18
解析: 满足几何分布,∴Eξ=np=14.7.
∴B满足.
答案: B
9.满足不等式0≤y≤2-|x|的整数解(x,y)的个数是
A.6 B.7 C.8 D.9
解析: 由已知|x|≤2,则-2≤x≤2.
当x=-2,2时,y=0.有2个;
当x=-1,1时,y=0,1.有4个;
当x=0时,y=0,1,2.有3个.
综上,共有9个,故选D.
答案: D
8.如果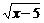 ≠kx对一切x≥15均成立,则有
≠kx对一切x≥15均成立,则有
A.k≤0 B.k≤0或k>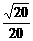 C.k≤0或k>
C.k≤0或k>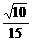 D.0≤k<
D.0≤k<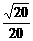
解析: 令y=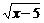 ,y=kx,显然k≤0时成立,
,y=kx,显然k≤0时成立,
由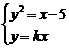
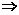 k2x2-x+5=0(k>0),
k2x2-x+5=0(k>0),
由Δ=0,得k=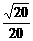 ;
;
由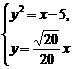 得x=10,而x≥15,
得x=10,而x≥15,
∴当x=15时,k=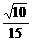 .
.
∴k≤0或k>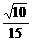 .
.
答案: C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com