18.(12分)(2003年高考新课程卷)设a＞0，求函数f(x)=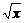－ln(x+a)(x∈(0，+∞))的单调区间.

分析：本小题主要考查导数的概念和计算，应用导数研究函数性质的方法及推理和运算能力.

解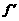：(x)=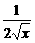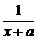－(x＞0).

当a＞0，x＞0时，

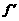(x)＞0x²+(2a－4)x+a²＞0，

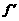(x)＜0x²+(2a－4)x+a²＜0.

①当a＞1时，对所有x＞0，有x²+(2a－4)x+a²＞0，即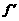(x)＞0.

此时f(x)在(0，+∞)内单调递增.

②当a=1时，对x≠1，有x²+(2a－4)x+a²＞0，

即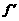(x)＞0，此时f(x)在(0，1)内单调递增，在(1，+∞)内单调递增.

又知函数f(x)在x=1处连续.

因此，函数f(x)在(0，+∞)内单调递增.

③当0＜a＜1时，令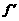(x)＞0，即

x²+(2a－4)x+a²＞0，解得x＜2－a－2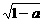，或x＞2－a+2.

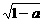因此，函数f(x)在区间(0，2－a－2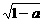)内单调递增，在区间(2－a+2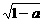，+∞)内也单调递增.

令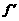(x)＜0，即x²+(2a－4)x+a²＜0，解得2－a－2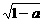＜x＜2－a+2.

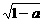因此，函数f(x)在区间(2－a－2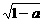，2－a+2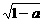)内单调递减.

17.(12分)函数y=lg(3－4x+x²)的定义域为M，x∈M时，求f(x)=2^x+2－3×4^x的最值.

解：由3－4x+x²＞0得x＞3或x＜1，

∴M={x|x＞3或x＜1}，

f(x)=－3×2^2x+2²·2^x=－3(2^x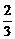－)²+.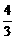

∵x＞3或x＜1，

∴2^x＞8或0＜2^x＜2.

∴当2^x=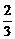即x=log₂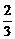时，f(x)最大，最大值为.

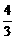f(x)没有最小值.

16.对于函数y=f(x)(x∈R)，有下列命题：

①在同一坐标系中，函数y=f(1+x)与y=f(1－x)的图象关于直线x=1对称；

②若f(1+x)=f(1－x)，且f(2－x)=f(2+x)均成立，则f(x)为偶函数；

③若f(x－1)=f(x+1)恒成立，则y=f(x)为周期函数；

④若f(x)为单调增函数，则y=f(a^x)(a＞0，且a≠1)也为单调增函数.

其中正确命题的序号是______________.

(注：把你认为正确命题的序号都填上)

解析：①不正确，y=f(x－1)与y=f(1－x)关于直线x=1对称.②正确.③正确.④不正确.

答案：②③

15.(2004年春季上海)已知函数f(x)=log₃(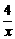+2)，则方程f^－1(x)=4的解x=___________________.

解析：由f^－1(x)=4，得x=f(4)=log₃(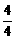+2)=1.

答案：1

14.设函数f(x)的定义域是N^*，且f(x+y)=f(x)+f(y)+xy，f(1)=1，则f(25)= ___________________.

解析：由f(x+y)=f(x)+f(y)+xy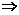f(2)=f(1)+f(1)+1=3.

∴f(2)－f(1)=2.

同理，f(3)－f(2)=3.

……

f(25)－f(24)=25.

∴f(25)=1+2+3+…+25=325.

答案：325

13.(2004年浙江，理13)已知f(x)=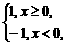则不等式x+(x+2)·f(x+2)≤5的解集是___________________.

解析：当x+2≥0时，原不等式x+(x+2)≤5x≤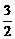.∴－2≤x≤.

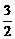当x+2＜0时，原不等式x+(x+2)(－1)≤5－2≤5.∴x＜－2.

综上，知x≤.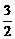

答案：(－∞，］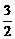

12.方程log₂(x+4)=3^x实根的个数是

A.0　 　　　　　　　　　　　　　 B.1　　　　　　　　　　　　　　　 C.2　 　　　　　　　　　　　　　 D.3

解析：设y=log₂(x+4)及y=3^x.

画图知交点有两个.

答案：C

11.偶函数y=f(x)(x∈R)在x＜0时是增函数，若x₁＜0，x₂＞0且|x₁|＜|x₂|，下列结论正确的是

A.f(－x₁)＜f(－x₂)　　　　　　　　　　　　　　　　　 B.f(－x₁)＞f(－x₂)

C.f(－x₁)=f(－x₂)　　　　　　　　　　　　　　　　　　 D.f(－x₁)与f(－x₂)大小关系不确定

解析：|x|越小，f(x)越大.∵|x₁|＜|x₂|，∴选B.

答案：B

10.设函数f(x)=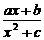的图象如下图所示，则a、b、c的大小关系是

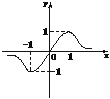
A.a＞b＞c　　　　　　　　　　 B.a＞c＞b　　　　　　　　　　 C.b＞a＞c　　　　　　　　　　 D.c＞a＞b

解析：f(0)=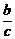=0，∴b=0.

f(1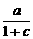)=1，∴=1.

∴a=c+1.由图象看出x＞0时，f(x)＞0，即x＞0时，有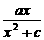＞0，∴a＞0.又f(x)= 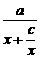，当x＞0时，要使f(x)在x=1时取最大值1，需x+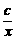≥2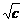，当且仅当x=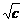=1时.∴c=1，此时应有f(x)=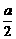=1.

∴a=2.

答案：B

9.(2004年全国Ⅳ，12)设函数f(x)(x∈R)为奇函数，f(1)=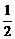，f(x+2)=f(x)+

f(2)，则f(5)等于

A.0　　　　　　　　　　　　　　　 B.1　　　　　　　　　　　　　　　 C.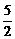　　　　　　　　　　　　　　　　　 D.5

解析：∵f(x+2)=f(x)+f(2)且f(x)为奇函数，f(1)=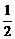，∴f(1)=f(－1+2)=

f(－1)+f(2)=－f(1)+f(2).∴f(2)=2f(1)=1.∴f(5)=f(3)+f(2)=f(1+2)+ f(2)=f(1)+2f(2)=.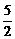

答案：C