
题目列表(包括答案和解析)
5.(山东卷)定义集合运算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为
(A)0 (B)6 (C)12 (D)18
解:当x=0时,z=0,当x=1,y=2时,z=6,当x=1,y=3时,z=12,故所有元素之和为18,选D
3.(广东卷)对于任意的两个实数对 和
和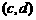 ,规定:
,规定: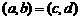 ,当且仅当
,当且仅当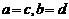 ;运算“
;运算“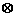 ”为:
”为: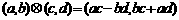 ;运算“
;运算“ ”为:
”为: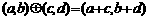 ,设
,设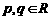 ,若
,若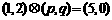 ,则
,则
A.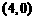 B.
B. 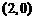 C.
C. 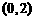 D.
D. 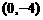
解析:由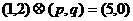 得
得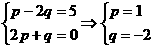 ,
,
所以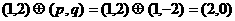 ,故选B.
,故选B.
2. (福建卷)对于直角坐标平面内的任意两点A(x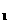 ,
, y
y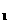 )、B(x
)、B(x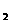 ,y
,y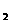 ),定义它们之间的一种“距离”:‖AB‖=︱x
),定义它们之间的一种“距离”:‖AB‖=︱x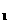 -x
-x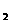 ︱+︱y
︱+︱y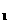 -y
-y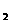 ︱.给出下列三个命题:
︱.给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖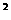 +‖CB‖
+‖CB‖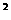 =‖AB‖
=‖AB‖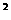 ;
;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题的个数为
A.0 B.1 C.2 D.3
解析:对于直角坐标平面内的任意两点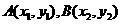 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: 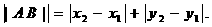 ①若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,则
①若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,则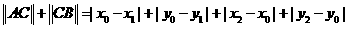 =
=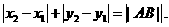
③在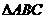 中,
中,
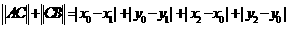 >
>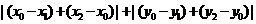
=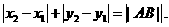 ∴命题① ③成立,而命题②在
∴命题① ③成立,而命题②在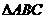 中,若
中,若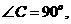 则
则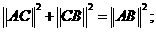 明显不成立,选B.
明显不成立,选B.
1. (北京卷)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口
(北京卷)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口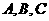 的机动车辆数如图所示,图中
的机动车辆数如图所示,图中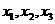 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段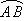 、
、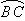 、
、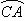 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A)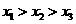 (B)
(B)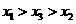 (C)
(C)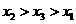 (D)
(D)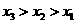
解:依题意,有x1=50+x3-55=x3-5,\x1<x3,同理,x2=30+x1-20=x1+10\x1<x2,同理,x3=30+x2-35=x2-5\x3<x2故选C
8.在所有定周长的空间四边形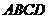 中,求对角线
中,求对角线 和
和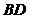 的最大值,并证明.
的最大值,并证明.
7.已知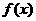 满足:对实数
满足:对实数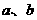 有
有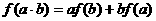 ,且
,且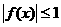 ,求证
,求证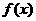 恒为零.
恒为零.
(可用以下结论:若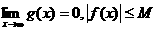 ,
,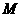 为一常数,那么
为一常数,那么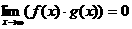 )
)
6.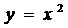 上一点
上一点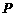 (非原点),在P 处引切线交
(非原点),在P 处引切线交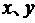 轴于
轴于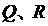 ,求
,求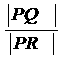 .
.
5.随机取多少个整数,才能有0.9以上的概率使得这些数中至少有一个偶数.
4.求由正整数组成的集合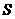 ,使
,使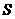 中的元素之和等于元素之积.
中的元素之和等于元素之积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com