
题目列表(包括答案和解析)
1. 不等式 | x + 3 | > x + 3 的解是 ( )
(A) x > 0 (B) x < 0 (C) x <-3 (D) x £ -3
20. (本小题满分14分)
(1) 由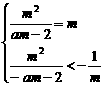 , 得
, 得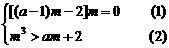 2分
2分
由(1)得 m
= 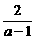 ,
,
当a = 2时, m = 2, 满足(2)式;
当a = 3时, m
= 1, 不满足(2)式, 舍去. 得f ( x ) = 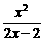 ( x ¹ 1).
3分
( x ¹ 1).
3分
(2) 由条件得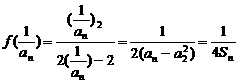
∴ an(1 – an) = 2Sn (3) , 2分
令n = 1,得 a1 = –1,
又an – 1 (1 – an – 1 ) = 2S n – 1 , ∴( an + a n – 1 )( an + 1 – a n – 1 )= 0,
由an – a n – 1 = – 1 , a1 = –1,得{an}是首项为– 1, 公差为– 1的等差数列,
∴ an= – 1 + (n – 1 )( – 1)= – n . 3分
(3) 由(2)知,满足条件的数列不惟一.
考虑到a1 ¹ 1, 由 an = – a n – 1 及an – a n – 1 = – 1和a1 = –1,
构造数列{ –1, –2, 2,–2, –3, – 4, … , – n +2, … }. 2分
用数学归纳法证明,该数列满足(3)式,
当n = 1, 2, 3, 4, 5时,直接代入可得(3)式成立,
假设n = k ( k ³ 5)时,(3)成立, 则n = k + 1时,
Sk+1 =S k + a k+1
= 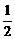 ak(1 – ak) + a k + 1 =
ak(1 – ak) + a k + 1 = 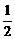 (–a k +1)(1 + ak+1) + a k + 1 =
(–a k +1)(1 + ak+1) + a k + 1 =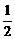 ak+1(1 – a k+1).
ak+1(1 – a k+1).
所以n = k + 1时(3)式成立, 即该数列满足题设条件.
得满足条件的数列不惟一.
构造数列也可能是:
{ –1, 1, –1, –2, –3, – 4, … , – n , … };
{ –1, –2,2, –2, 2, –2, … , (–1) n – 1 2 , … }( n > 1 )
{ –1, –2,2, –2, –3, – 4, … , – n , … }等等.
19. (本小题满分14分)
(1)
|
长度ξμm |
29 |
30 |
31 |
|
P |
0.3 |
0.5 |
0.2 |
|
宽度ημm |
19 |
20 |
21 |
|
P |
0.3 |
0.4 |
0.3 |
4分
(2)P(ζ = 96) = 0.3´0.3 = 0.09;
P(ζ = 98) = 0.3´0.4 + 0.5´0.3 = 0.27;
P(ζ = 100) = 0.5´0.4 + 0.2´0.3 + 0.3´0.3 = 0.35;
P(ζ = 102) = 0.2´0.4 + 0.5´0.3 = 0.23;
P(ζ = 104) = 0.2´0.3 = 0.06.
得,周长分布律如下表所示
|
周长μ μm |
96 |
98 |
100 |
102 |
104 |
|
P |
0.09 |
0.27 |
0.35 |
0.23 |
0.06 |
6分
(3)方法1(利用周长的分布计算)
Eμ= 96×0.09+98×0.27+100×0.35+102×0.23+104×0.06=99.8 4分
方法2(利用矩形长与宽的期望计算)
由长和宽的分布率可以算得
Eξ=29×P(ξ=29)+30×P(ξ=30)+31×P(ξ=31)
=29×0.3+30×0.5+31×0.2=29.9
Eη=19×P(η=19)+20×P(η=20)+21×P(η=21)
=19×0.3+20×0.4+21×0.3=20
由期望的性质可得
Eμ=2(Eξ+Eη)=2×(29.9+20)=99.8 4分
18. (本小题满分14分)
解:
(1) P(x) = R (x) – C (x) = – 10x3 + 45x2 + 3240x – 5000 (xÎN且xÎ[1, 20]); 2分
MP (x) = P ( x + 1 ) – P (x) = – 30x2 + 60x +3275 (xÎN且xÎ[1, 20]). 2分
(2) P`(x) = – 30x2 + 90x + 3240 = – 30( x +9 )(x – 12) (xÎN且xÎ[1, 20]) 3分
当1< x < 12时, P`(x) > 0, P(x)单调递增,
当 12 <x < 20时, P`(x) < 0 , P ( x ) 单调递减.
∴ x = 12 时, P(x)取最大值, 3分
即, 年建造12艘船时, 公司造船的年利润最大. 1分
(3) 由MP(x ) = – 30( x – 1) 2 + 3305 (xÎN且xÎ[1, 20]).
∴当1< x £ 20时,MP (x)单调递减. 2分
MP (x)是减函数说明: 随着产量的增加,每艘利润与前一台比较,利润在减少.1分
17.(本小题满分14分)
解1: |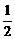 a -
a - 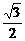 b |2 = |
(
b |2 = |
(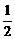 sinx–
sinx–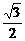 cosx, -
cosx, -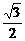 ) |2
2分
) |2
2分
= (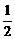 sinx–
sinx–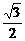 cosx)2 +
cosx)2 +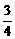 3 分
3 分
= sin2(x – 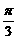 ) +
) +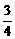 .
3分
.
3分
Π0 < x
< 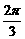 , ∴–
, ∴–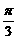 < x -
< x -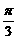 <
< 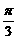 ,
2分
,
2分
∴ 0 £ sin2(C–
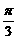 ) <
) < 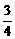 ,
2分
,
2分
得 |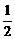 a -
a -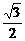 b | Î [
b | Î [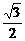 ,
, 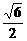 ).
2分
).
2分
解2: |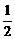 a –
a – 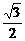 b |2 =
b |2 = 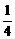 | a |2 –
| a |2 – 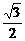 a·b +
a·b + 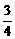 | b |2
2分
| b |2
2分
= 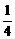 sin2 –
sin2 –
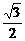 sinxcosx +
sinxcosx + 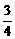 (cos2x +1)
2分
(cos2x +1)
2分
=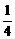 sin2–
sin2–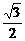 sinxcosx +
sinxcosx + 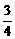 cos2x +
cos2x + 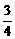
= (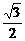 cosx –
cosx – 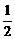 sinx)2 +
sinx)2 +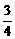 2 分
2 分
= sin2(x – 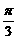 ) +
) +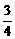 .
2分
.
2分
Π0 < x
< 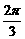 , ∴–
, ∴–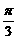 < x -
< x -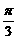 <
< 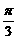 ,
2分
,
2分
∴ 0 £ sin2(C–
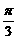 ) <
) < 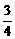 ,
2分
,
2分
得|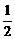 a -
a - 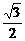 b |2 Î [
b |2 Î [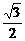 ,
, 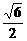 ).
2分
).
2分
16. (本小题满分14分)
由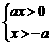 ,得a > 0 , x > 0 . 3
分
,得a > 0 , x > 0 . 3
分
不等式化成: lg(2ax) < lg(10a + 10x) 3分
得2ax < 10a + 10x
(a – 5)x < 5a 2分
当 0 < a < 5时, a – 5 < 0, 解得x >0, 2分
当 a = 5时,不等式为0•x < 25, 得x > 0, 2分
当 a > 5时, a – 5 > 0, 解得0 < x <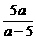 . 2分
. 2分
15. (本小题满分14分)
由(b + c)x 2 –2ax + (b – c ) = 0有相等实根,
得 ⊿= 4a 2 – 4( b + c )(b – c) = 0, 3分
即 a 2 + c 2 – b 2 = 0 ,
∴ B = 90° . 3分
又sinCcosA – cosCsinA=0 ,
得 sin (C – A) = 0 . 2分
∵–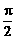 < C – A <
< C – A < 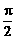 ,
2分
,
2分
∴ A = C,
∴△ABC是B为直角的等腰直角三角形. 2分
13. 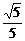 . 14. 0 < a £
. 14. 0 < a £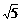 – 2 (或q < x £ p , 其中q > 0, p£
– 2 (或q < x £ p , 其中q > 0, p£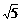 – 2)
.
– 2)
.
11. (–¥ ,3] . 12
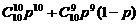 .
.
(17)(本小题满分12分)
一出租车司机从某饭店到火车站途中有六个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是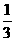 .
.
(1) 求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(2)
求这位司机遇到红灯数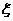 的期望与方差.
的期望与方差.
(18)(本小题满分12分)
已知向量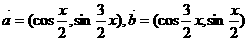 且
且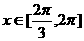 .
.
(1)
求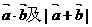 ;
;
(2)
求函数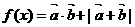 的最值.
的最值.
(19)(本小题满分12分,以下两题选做一题,若甲,乙都做,只按甲题计分)
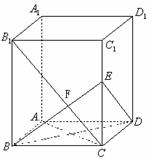
(甲)长方体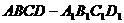 中,
中,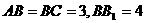 连接
连接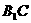 过B作
过B作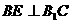 交
交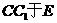 ,交
,交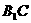 于F.
于F.
(1)
求证: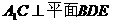 ;
;
(2)
求三棱锥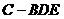 的体积;
的体积;
(3)
求二面角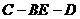 的正切值.
的正切值.
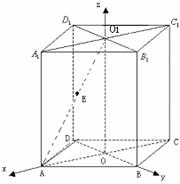
(乙)直四棱柱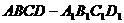 的高为6,底面是边长为4,
的高为6,底面是边长为4,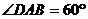 的菱形,
的菱形,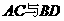 相交于
相交于 点,
点, 与
与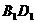 相交于
相交于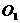 点,点
点,点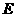 是
是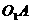 的中点.
的中点.
(1)
求二面角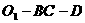 的大小;
的大小;
(2)
分别以射线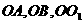 为
为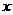 轴,
轴,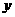 轴,
轴,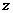 轴的正半轴建立空间直角坐标系,求点
轴的正半轴建立空间直角坐标系,求点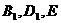 的坐标,并求异面直线
的坐标,并求异面直线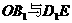 所成角的大小.
所成角的大小.
(20)(本小题满分12分)
我国北方某城市严重缺水,曾一度取消全市的洗车行业.时间久了,车容影响了市容市貌.今年该市决定引进一种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车.污水净化器的价格是每台100万元,全市统一洗车价格10元.该市今年的汽车总量是101000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是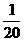 x,该洗车行每年的其他费用是1万元.问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?
x,该洗车行每年的其他费用是1万元.问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?
(21)(本小题满分12分)
已知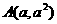 为抛物线
为抛物线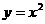 上任意一点,直线
上任意一点,直线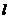 为过点
为过点 的切线,设直线
的切线,设直线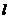 交
交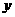 轴于点
轴于点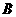 .
.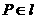 ,且
,且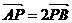 .
.
(1)
当 点运动时,求点
点运动时,求点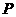 的轨迹方程;
的轨迹方程;
(2)
求点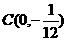 到动直线
到动直线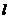 的最短距离,并求此时
的最短距离,并求此时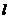 的方程.
的方程.
(22)(本小题满分14分,文科学生做(1),(2),理科学生做(1),(2),(3))
已知函数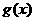 与函数
与函数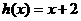 图像关于
图像关于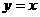 对称.且函数
对称.且函数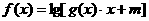 ,(其中
,(其中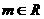 ,
, 为常数)
为常数)
(1)
求函数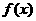 的定义域;
的定义域;
(2)
问是否存在实数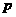 ,使得
,使得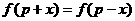 ,若存在,请求出
,若存在,请求出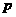 ,若不存在,说明理由;
,若不存在,说明理由;
(3)
函数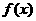 的定义域与值域能否同时为实数集
的定义域与值域能否同时为实数集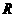 ?并证明你的结论.
?并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com