
题目列表(包括答案和解析)
3.直线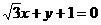 的倾斜角为( )
的倾斜角为( )
(A)150° (B)120° (C)60° (D)-60°
2.设a、b、c、d∈R,且a>b,c>d则下列一定成立的不等式为( )
(A)a-c<b-d
(B)ac>bd
(C)a-d>b-c
(D)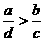
1.若a<0,b>0,且a+b<0,则下列不等式中成立的是( )
(A)-b<a<b<-a
(B)-b<a<-a<b
(C)a<-b<b<-a
(D)a<-b<-a<b
22、(本小题满分14分)
已知二次函数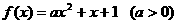 的图象与x轴交点的横坐标分别为
的图象与x轴交点的横坐标分别为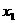 、
、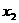 .
.
(1)证明: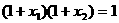 ;
;
(2)证明: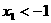 ,
,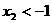 ;
;
(3)若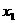 、
、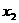 满足不等式
满足不等式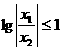 ,试求
,试求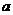 的取值范围.
的取值范围.
(1); (2)证明略
(3)解:
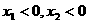 ∴ 由
∴ 由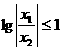 得
得 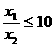
∴ 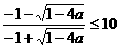 ∴
∴ 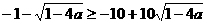
∴ 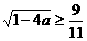 ∴
∴ 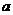 的取值范围是
的取值范围是 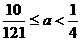 .
.
20. (本小题满分12)
(本小题满分12)
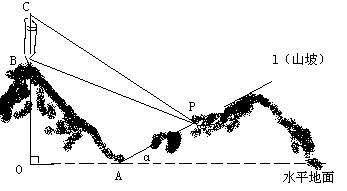
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线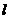 且点P在直线
且点P在直线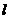 上,
上,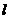 与水平地面的夹角为a ,tana =
与水平地面的夹角为a ,tana =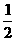 ,试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高).
,试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高).
解:以OA所在直线为x轴,O为原点建立平面直角坐标系,
则A(200,0),B(0,220),C(0,300),
直线l的方程为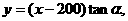 即
即
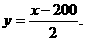 设点P的坐标为(x,y),
设点P的坐标为(x,y),
则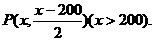
由经过两点的直线的斜率公式 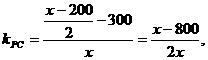
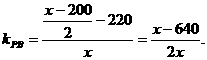
由直线PC到直线PB的角的公式得
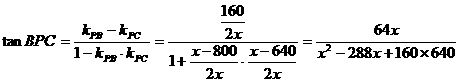
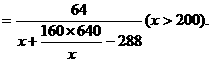
要使tanBPC达到最大,只须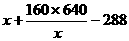 达到最小,由均值不等式
达到最小,由均值不等式
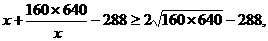
当且仅当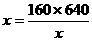 时上式取得等号,故当x=320时tanBPC最大,这时,点P的纵坐标y为
时上式取得等号,故当x=320时tanBPC最大,这时,点P的纵坐标y为
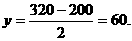
由此实际问题知,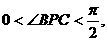 所以tanBPC最大时,∠BPC最大,故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大.
所以tanBPC最大时,∠BPC最大,故当此人距水平地面60米高时,观看铁塔的视角∠BPC最大.
(21)(本小题共12分)
设数列{an}的首项a1=a≠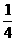 ,且
,且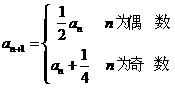 ,
,
记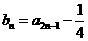 ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求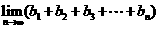 .
.
解:(I)a2=a1+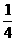 =a+
=a+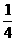 ,a3=
,a3=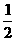 a2=
a2=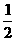 a+
a+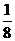 ;
;
(II)∵ a4=a3+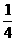 =
=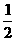 a+
a+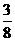 , 所以a5=
, 所以a5=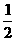 a4=
a4=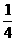 a+
a+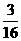 ,
,
所以b1=a1-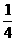 =a-
=a-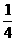 , b2=a3-
, b2=a3-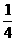 =
=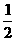 (a-
(a-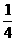 ), b3=a5-
), b3=a5-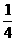 =
=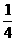 (a-
(a-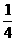 ),
),
猜想:{bn}是公比为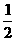 的等比数列·
的等比数列·
证明如下:
因为bn+1=a2n+1-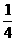 =
=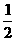 a2n-
a2n-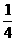 =
=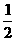 (a2n-1-
(a2n-1-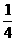 )=
)=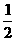 bn, (n∈N*)
bn, (n∈N*)
所以{bn}是首项为a-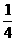 , 公比为
, 公比为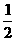 的等比数列·
的等比数列·
(III)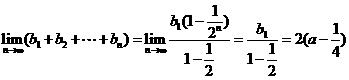
19.(本小题满分12分)
求满足下列条件的直线方程:
(1)通过点(-2,2),且与两坐标轴所围成的面积为1的直线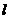 的方程;
的方程;
(2)已知直线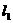 :
: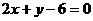 和点A(1,-1),过点A作直线
和点A(1,-1),过点A作直线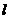 与已知直线
与已知直线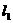 相交于B点,且|AB|=5,求直线
相交于B点,且|AB|=5,求直线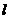 的方程.
的方程.
. 答案:(1)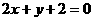 或
或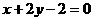
(2) 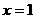 或
或 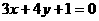
18.(本小题满分12分)
已知向量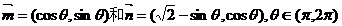
且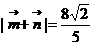 ,求
,求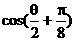 的值.
的值.
解法一:
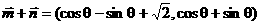
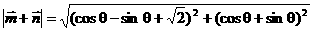
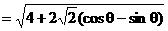
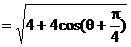
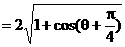
由已知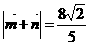 ,得
,得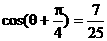
又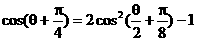
所以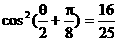
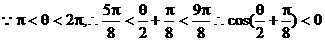
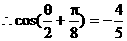
解法二:
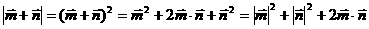

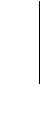
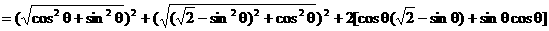
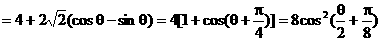
由已知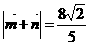 ,得
,得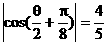
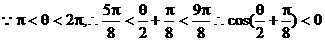
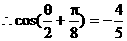
17.(本小题满分12分)
设函数f (x)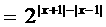 , 求使f(x)≥
, 求使f(x)≥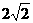 的x取值范围.
的x取值范围.
答案: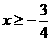
15. 16.
13. 14.
14.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com