
题目列表(包括答案和解析)
3. 集合间的关系
判断下列两集合之间的关系
⑴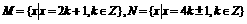
(2)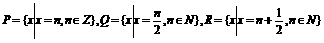
(3)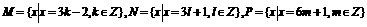
(4)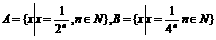
(5)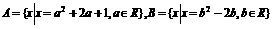
(6)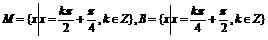
2. 集合中元素的个数
(1) 已知集合M,N分别含有8个、13个元素,若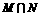 中有6个元素, ①求
中有6个元素, ①求 中的元素个数. ②当
中的元素个数. ②当  含多少个元素时,
含多少个元素时,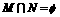 .
.
(2) 对某城市1000户的居民生活水平进行调查,统计结果有彩电的有682户,有电冰箱的有819户, 彩电和电冰箱二者都有的535户,问彩电和电冰箱至少有一种的有多少户。
(3) 某文艺小组共有10名成员,每人至少会唱歌和跳舞中的一项,其中7人会唱歌跳舞5人会,现从中选出会唱歌和会跳舞的各一人,表演一个唱歌和一个跳舞节目,问有多少种不同的选法?
(4) 某运动队有10名赛艇运动员,其中7人会划左桨,6人会划右桨,要选出6名运动员参加比赛,其中3名左桨选手,3名右桨选手,问有多少种不同的组队方案?
(5) 某班一天排7节不同的课,要求体育课不排第一节,语文课不排第七节,问有多少种不同的排法?(只列式,不计算)
1. 子集的个数
(1)
若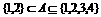 ,求满足这个关系式的集合A的个数
,求满足这个关系式的集合A的个数
(2)
已知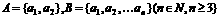 ①求集合
①求集合 的子集个数 ②求满足条件
的子集个数 ②求满足条件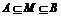 的集合
的集合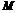 的个数
的个数
12. 解:由已知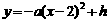 ,
,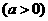 . ∴
. ∴ 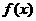 在(-∞,
在(-∞,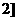 上单增,在(2,+∞)上单调.
上单增,在(2,+∞)上单调.
又∵ 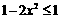 ,
,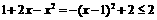 .
.
∴ 需讨论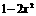 与
与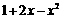 的大小.
的大小.
由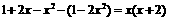 知
知
当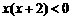 ,即
,即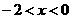 时,
时,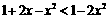 .
.
故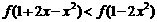 时,应有
时,应有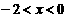
11. 解:(1)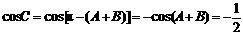 ,
,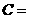 120°
120°
(2)∵ a,b是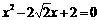 的两个根,
的两个根,
∴ 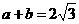 ,
,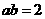
∴ 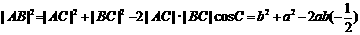
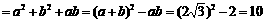 ∴
∴ 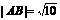
(3)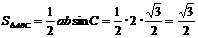
10. 解:由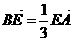 ,
,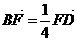 ,可直接求得
,可直接求得 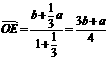 ,
,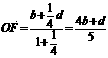 .
.
∴ 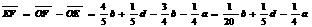
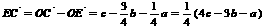 .
.
由平行四边形性质,知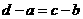 . 即
. 即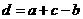
所以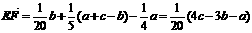
∴  ,从而E、F、C三点共线.
,从而E、F、C三点共线.
9. 设点B的坐标为(x,y),则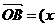 ,
,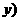 ,
,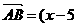 ,
,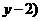 ∵
∵ 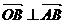
∴ 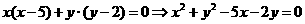 ①
①
又∵ 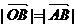 ∴
∴ 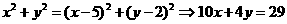 ②
②
解①②得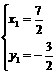 或
或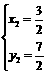
∴ 点B的坐标为( ,
,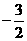 )或(
)或(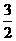 ,
, )
)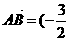 ,
,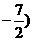 或
或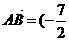 ,
,
8. (1)如图,在平面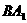 内,过
内,过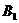 作
作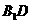 ⊥AB于D, ∵ 侧面
⊥AB于D, ∵ 侧面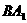 ⊥平面ABC,
⊥平面ABC,
∴ 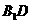 ⊥平面ABC,
⊥平面ABC,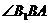 是
是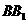 与平面ABC所成的角,∴
与平面ABC所成的角,∴ 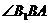 =60°.
=60°.
∵ 四边形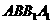 是菱形, ∴ △
是菱形, ∴ △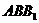 为正三角形,
为正三角形,
∴ D是AB的中点,即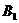 在平面ABC上的射影为AB的中点.
在平面ABC上的射影为AB的中点.
(2)连结CD,∵ △ABC为正三角形,
又∵ 平面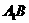 ⊥平面ABC,平面
⊥平面ABC,平面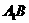
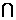 平面ABC=AB,
平面ABC=AB,
∴ CD⊥平面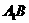 ,在平面
,在平面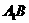 内,过D作DE⊥
内,过D作DE⊥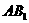 于E,连结CE,则CE⊥
于E,连结CE,则CE⊥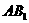 ,
,
∴ ∠CED为二面角C-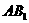 -B的平面角.在Rt△CED中,
-B的平面角.在Rt△CED中,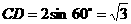 ,连结
,连结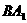 于O,则
于O,则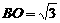 ,
,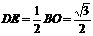 ,
,
∴ 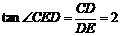 . ∴ 所求二面角C-
. ∴ 所求二面角C-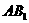 -B的大小为arctan2.
-B的大小为arctan2.
(3)答: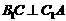 ,连结
,连结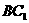 , ∵
, ∵ 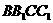 是菱形 ∴
是菱形 ∴ 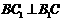
∴ CD⊥平面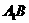 ,
,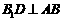 , ∴
, ∴ 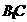 ⊥AB,
⊥AB,
∴ 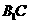 ⊥平面
⊥平面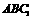 , ∴
, ∴ 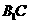 ⊥
⊥ .
.
7. 解:(1)设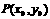 ,
,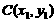 ,
,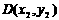 ,又
,又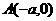 ,
,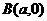 ,
,
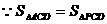 ,
, C为AP的中点,即
C为AP的中点,即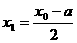 ,
,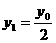 ,
,
代入椭圆方程得: ①; 又
①; 又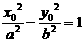 ②
②
①+②得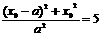 ,即
,即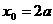
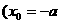 舍去),代入(2),并注意
舍去),代入(2),并注意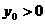 ,得
,得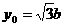 .
.
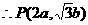 ,从而
,从而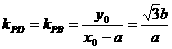 .
.
 直线PD方程为
直线PD方程为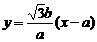 ,代入椭圆方程得:
,代入椭圆方程得: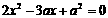 ,
,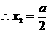
 ,
,
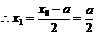 ,
,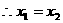 ,即
,即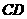 ⊥
⊥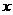 轴,
轴,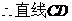 倾角为90°.
倾角为90°.
(2)当CD过椭圆右焦点时,有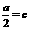 ,
,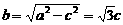 ,
,
在双曲线中,半焦距 ,半实轴
,半实轴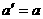 ,
,
 双曲线离心率
双曲线离心率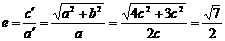 ,
,
此时,CD恰好过椭圆右焦点.
∴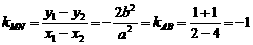 ,以下同法一。
,以下同法一。
(2)由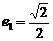 ,
,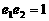 得
得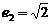 ,即
,即 ,∴
,∴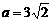 或
或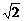 。
。
当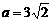 时,b2=9,椭圆方程为
时,b2=9,椭圆方程为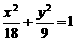 ;
;
当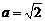 时,b2=1,代入(*)知Δ<0,不合题意,舍去;
时,b2=1,代入(*)知Δ<0,不合题意,舍去;
(另法:此时A(-2,1)在椭圆外,不可能为弦MN中点,舍去)
∴椭圆C1方程只能为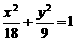 。
。
以下法一:将a2=18,b2=9,代入(*)得x2+4x=0,∴x1+x2=-4,x1x2=0,
∴|MN|=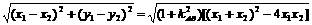
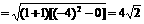 ,
,
又|AB|=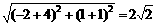
∴|MB|=|MA|+|AB|=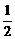 |MN|+|AB|=2
|MN|+|AB|=2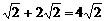 .
.
以下法二:具体求出M、N点的坐标。
以下法三:先验证点B(-4,-1)在椭圆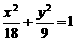 上,即B与N重合,从而|MB|=|MN|,故转化为求弦长|MN|即可。
上,即B与N重合,从而|MB|=|MN|,故转化为求弦长|MN|即可。
6. 解:(1)
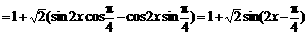
所以函数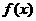 的最小正周期为
的最小正周期为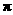 ,最大值为
,最大值为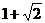 .
.
(2)由(1)知
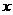 |
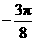 |
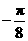 |
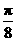 |
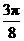 |
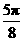 |
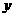 |
1 |
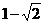 |
1 |
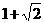 |
1 |
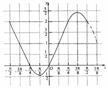 故函数
故函数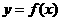 在区间
在区间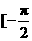 ,
,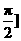 上的图像是
上的图像是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com