
题目列表(包括答案和解析)
18. (1)由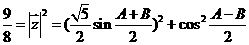 ,得
,得
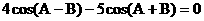 ,即
,即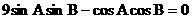
∴ =
=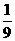 (定值)……………….5分
(定值)……………….5分
(2)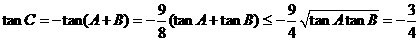 ……8分
……8分
当且仅当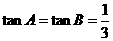 时,
时,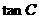 最大.
最大.
设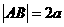 ,由
,由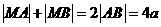 知,动点M在以AB为焦点的圆上,
知,动点M在以AB为焦点的圆上,
以AB的中点为原点,直线AB为x轴建立直角坐标系,则椭圆方程为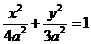 .
.
设M(x,y),则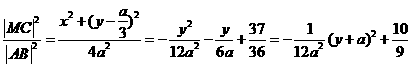 ,
,
∴当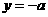 时,
时,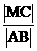 取最大值
取最大值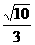 .…….12分
.…….12分
17、(1)取AC的中点E,连结DE、BE,则DE∥PC。∵PC⊥AC,∴AC⊥DE,又AC⊥BE,∴AC⊥平面BDE,∴AC⊥BD.……5.分
(2)∵AC⊥平面BDE,∴平面BDE⊥平面ABC∴BE是BD在底面ABC上的射影 ∴∠DBE为BD与底面ABC所成的角.….8分
又∵DE⊥AC,BE⊥AC,∴∠BED是二面角P-AC-B的平面角,即∠BED=120°,在△BDE中,由正弦定理得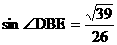 ……12分
……12分
14.由题意可得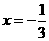 .
.
13、 . 14、
. 14、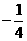 . 15、0.2 . 16、②③.
. 15、0.2 . 16、②③.
提示:
12.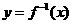 为“上凸”的函数.
为“上凸”的函数.
5.由题意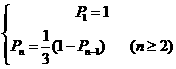
1-5 D A C A B
6-10 B D C A C
11-12 C B
提示:
3.由已知得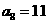 ,
,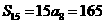 .
.
22.(本小题满分14分)
已知函数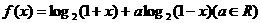 .
.
(1)函数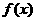 的图象关于原点对称的充要条件是什么?证明你的结论;
的图象关于原点对称的充要条件是什么?证明你的结论;
(2)对于满足(1)的函数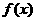 ,解关于x的不等式
,解关于x的不等式 ;
;
(3)证明:当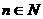 ,且
,且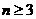 时,
时,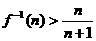 .
.
高三数学(四)参考解答及评分标准
21.(本小题满分12分)
已知椭圆的中心在原点,焦点在y轴上,离心率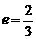 ,焦点到相应准线的距离为
,焦点到相应准线的距离为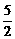 .
.
(1)求该椭圆的方程;
(2)P、Q是椭圆上的点,上焦点F在线段PQ上,且有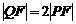 ,求P、Q所在直
,求P、Q所在直
线的方程.
20.(本小题满分12分)
已知函数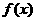 满足
满足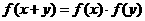 ,且
,且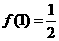 .
.
(1)当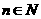 时,求
时,求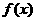 的表达式;
的表达式;
(2)设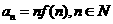 ,求证:
,求证: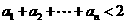 ;
;
(3)设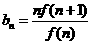 ,
,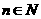 ,
,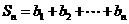 ,
,
求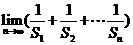 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com