
题目列表(包括答案和解析)
2、设向量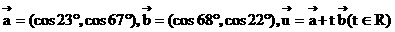 。
。
(1)求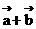 ;
;
(2)求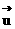 的模的最小值。
的模的最小值。
1、解:(1)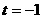 时,
时,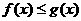 即为
即为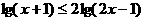 ,
,
此不等式等价于
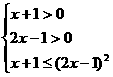 即
即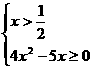 即
即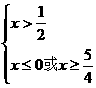
∴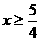
∴原不等式的解集为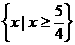 .
.
(2) 时,
时,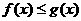 恒成立。
恒成立。
∴ 时,
时,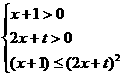 恒成立,∴
恒成立,∴ 时,
时,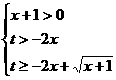 恒成立,
恒成立,
即 时,
时,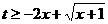 恒成立,于是转化为求
恒成立,于是转化为求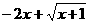 ,
,
 的最大值问题,令
的最大值问题,令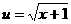 ,则
,则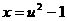 ,由
,由 ,知
,知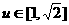
∴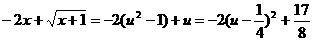 。
。
当u=1即x=0时,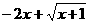 有最大值1,∴t的取值范围是
有最大值1,∴t的取值范围是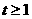 。
。
1、已知f(x)=lg(x+1),g(x)=2lg(2x+t)(t∈R,是参数),
(1)当t=-1时,解不等式f(x) ≤g(x);
(2)如果当x∈[0,1]时,f(x)≤g(x)恒成立,求参数t的取值范围。
9、解:(1)依题意:第n年共有5n个职工,那么基础工资总额为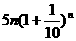 (万元),
(万元),
医疗费总额为5n×0.16=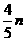 (万元),
(万元),
住房补贴为5×0.04n+5×0.04(n-1)+……+5×0.04×2+5×0.04=5×0.04(1+2+3+…+n)
=0.2×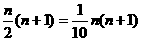 (万元).
(万元).
∴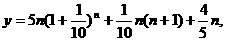
(2)假设可以超过,则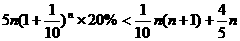
即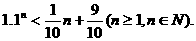
由函数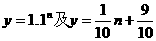 的图象知,上面不等式不能成立.
的图象知,上面不等式不能成立.
故住房补贴和医疗费总和不会超过基础工资总额的20%.
9、某公司取消福利分房和公费医疗,实行年薪制工资结构改革.该公司从2003年起,每人
的工资由三个项目组成,并按下表规定实施:
|
项 目 |
金额(元/人,年) |
计 算 方 法 |
|
基础工资 |
10000 |
考虑物价因素,从2003年(含2003年)起每年递增10%(与工龄无关) |
|
住房补贴 |
400 |
按职工到公司年限计算,每工作一年补贴400元 |
|
医 疗 费 |
1600 |
固定不变 |
如果该公司今年年初有5位职工,计划从明年起每年年初新招5名职工.
(1)若今年(2003年)算第一年,试把第n年该公司付给职工工资总额y(万元)表示成年限n的函数;
(2)试判断公司每年发给职工的工资总额中,住房补贴和医疗费的总和能否超过基础工资总额的20%,请说明理由.
8、解:易知 ,
,
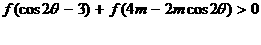
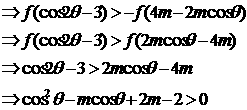

因此,满足条件的实数m存在,它可取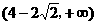 内的一切值。
内的一切值。
8、奇函数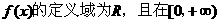 上是增函数,当
上是增函数,当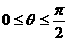 时,是否存在实数m,使
时,是否存在实数m,使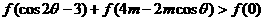 对所有的
对所有的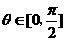 均成立?若存在,求出适合条件的所有实数m;若不存在,说明理由。
均成立?若存在,求出适合条件的所有实数m;若不存在,说明理由。
7、证明:(1)当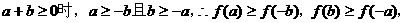
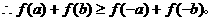
(2)(1)中命题的逆命题为: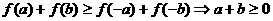 ①
①
①的逆否命题是: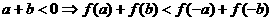 ②
②
仿(1)的证明可证②成立,又①与②互为逆否命题,故①成立,即(1)中命题的逆命题成立。
(1) 根据(2),所解不等式等价于
 。
。
7、已知函数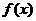 在R上是增函数,
在R上是增函数,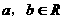 。
。
(1)
求证:如果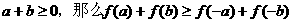 ;
;
(2) 判断(1)中的命题的逆命题是否成立?并证明你的结论;
(3)解不等式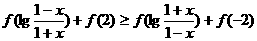 。
。
6、解:设建成x个球场,则每平方米的购地费用为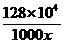 =
=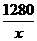
由题意知f(5)=400, f(x)=f(5)(1+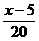 )=400(1+
)=400(1+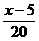 )
)
从而每平方米的综合费用为y=f(x)+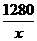 =20(x+
=20(x+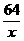 )+300≥20.2
)+300≥20.2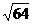 +300=620(元),当且仅当x=8时等号成立
+300=620(元),当且仅当x=8时等号成立
故当建成8座球场时,每平方米的综合费用最省.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com