
题目列表(包括答案和解析)
(13)已知数列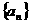 前
前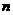 项和为
项和为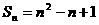 ,则
,则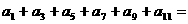 ____________________.
____________________.
(14)已知函数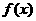 在R上连续,且
在R上连续,且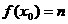
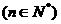 ,则
,则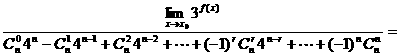 ____________-.
____________-.
(15)(理)复数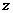 和
和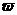 满足
满足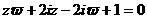 ,若
,若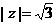 .则
.则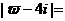 ______________.
______________.
(文)设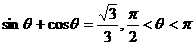 ,则
,则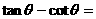 __________________.
__________________.
(16) 今年某校有4位报考艺术专业的学生参加艺术类的考试,同时该校有4名老师参加监考. 考试中心有10个考室,若要求该校任何两名考生不在同一考室,4位老师每两位必须在同一考室,但不得监考本校学生,则安排方法共有__________种.(结果用数据回答)
(1)
已知条件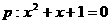 ,条件
,条件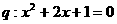 ,则
,则 的
的
(A) 充分不必要条件 (B)必要不充分条件
(C) 既不充分也不必要条件 (D)充要条件
(2)
设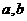 表示两条直线,
表示两条直线,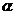 表示平面,给出下列四个命题
表示平面,给出下列四个命题
①若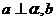 ∥
∥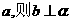
②若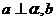 ∥
∥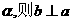
③若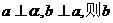 ∥
∥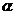
④若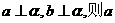 ∥
∥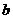
其中正确的命题个数是
(A) 1 (B) 2 (C)3 (D)4
(3)
若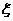 -
-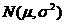 ,则下列说法正确的是
,则下列说法正确的是
(A) 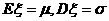 (B)
(B)
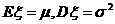
(C) 当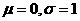 时,若总体小于
时,若总体小于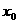 的取值为
的取值为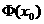 ,则
,则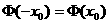
(D) 总体落在区间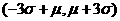 内的事件称为小概率事件.
内的事件称为小概率事件.
(4) 给出下列命题;
①若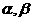 均为第一象限角,且
均为第一象限角,且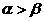 ,则
,则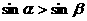 ;
;
②若函数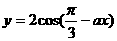 的最小正周期是
的最小正周期是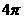 ,则
,则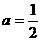 ;
;
③函数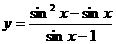 是奇函数;
是奇函数;
④函数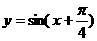 在
在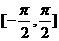 上是增函数.
上是增函数.
其中正确命题个数是
(A) 0 (B) 1 (C) 2 (D)3
(5)
曲线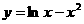 在点
在点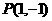 处的切线方程为
处的切线方程为
(A) 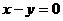 (B)
(B)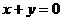
(C)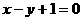 (D)
(D)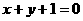
(6)
椭圆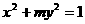 的焦点在
的焦点在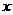 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的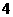 倍.则曲线
倍.则曲线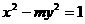 的离心率为
的离心率为
(A) 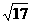 (B)
(B)
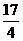 (C)
(C)
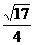 (D)
(D)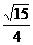
(7)
设函数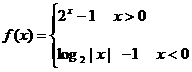 ,
,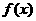 的反函数为
的反函数为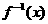 .则
.则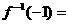
(A) 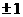 (B)
1 (C)
(B)
1 (C)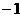 (D)2
(D)2
(8) 如图所示为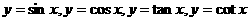 在
在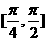 上的图像,则它们所对应的图像编号顺序是
上的图像,则它们所对应的图像编号顺序是
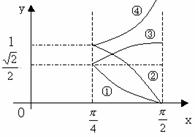
(A) ①②③④ (B) ①③②④ (C) ③①②④ (D) ③①④②
(9)
(理科)设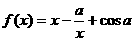 在
在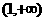 上总是增函数,则实数
上总是增函数,则实数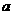 取值范围是
取值范围是
(A) 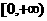 (B)
(B)
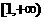 (C)
(C)
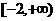 (D)
(D)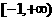
(文科)函数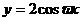 在区间
在区间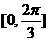 上递减,且有最小值1,则
上递减,且有最小值1,则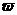 的值是
的值是
(A)2 (B)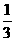 (C)3 (D)
(C)3 (D)
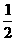
(10)(理科)已知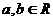 ,
,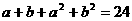 ,则
,则
(A) 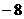 ≤
≤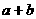 ≤6 (B)
≤6 (B)
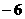 ≤
≤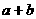 ≤8
≤8
(C) 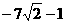 ≤
≤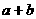 ≤
≤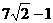 (D)
(D)
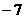 ≤
≤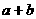 ≤7
≤7
(文科)若不等式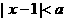 成立的充分条件是
成立的充分条件是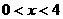 ,则实数
,则实数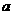 的取值范围是
的取值范围是
(A) 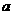 ≥3 (B)
≥3 (B)
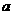 ≥1 (C)
≥1 (C)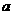 ≤1 (D)
≤1 (D)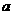 ≤3
≤3
(11)等比数列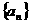 中,
中,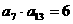 ,
,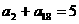 ,则
,则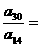
(A)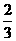 (B)
(B)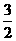 (C)
(C) (D)
(D)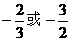
(12)若函数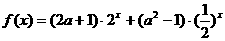 没有最小值,则实数
没有最小值,则实数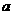 的取值范围是
的取值范围是
(A) 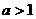 (B)
(B)
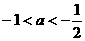 (C)
(C)
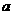 ≤1 (D)
≤1 (D)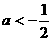
第Ⅱ卷(非选择题 共90分)
22.(本小题满分14分)
(理)已知函数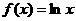
(1)求函数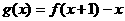 的最大值;
的最大值;
(2)当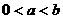 时,求证
时,求证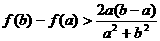 .
.
(文)设函数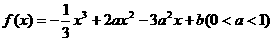
(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值;
(2)当x∈[a+1, a+2]时,不等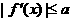 ,求a的取值范围.
,求a的取值范围.
21.(本小题满分12分)平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,
-2),点C满足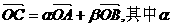 、
、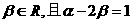
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线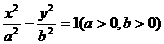 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: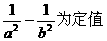 .
.
20.(本小题满分12分)如图,在底面是菱形的四棱锥P-ABCD中,
∠ABC=600,PA=AC=a,PB=PD=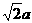 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(1)证明PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角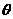 的大小;
的大小;
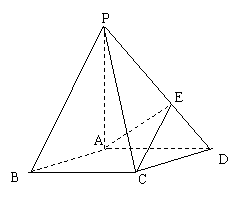 (3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
(3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
19.(本小题满分12分)
(理)已知函数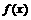 、
、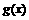 对任意实数
对任意实数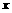 、
、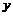 分别满足
分别满足
①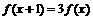 且
且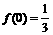 ;②
;②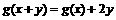 且
且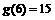 ,
,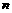 为正整数
为正整数
(1)求数列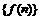 、
、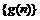 的通项公式;
的通项公式;
(2)设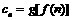 ,求数列
,求数列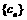 的前
的前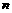 项和.
项和.
(文)已知等比数列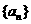 ,
,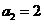 ,
,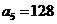
(1)求通项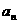 ;
;
(2)若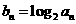 ,数列
,数列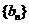 的前
的前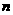 项的和为
项的和为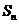 ,且
,且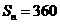 ,求
,求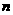 的值.
的值.
18.(本小题满分12分)
(理)某系统是由四个整流二极管(串、并)联结而成,已知每个二极管的可靠度为0.8
(即正常工作时),若要求系统的可靠度大于0.85,请你设计至少两种不同的联结方式,并说明理由.
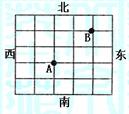 (文)如图是一个方格迷宫,甲、乙两人分别位于迷宫的A、B两处,现以每分钟一格的速度同时出发,在每个路口只能向东、西、南、北四个方向之一行走。若甲向东、向西行走的概率均为
(文)如图是一个方格迷宫,甲、乙两人分别位于迷宫的A、B两处,现以每分钟一格的速度同时出发,在每个路口只能向东、西、南、北四个方向之一行走。若甲向东、向西行走的概率均为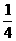 ,向南、向北行走的概率分别为
,向南、向北行走的概率分别为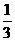 和p,乙向东、南、西、北四个方向行走的概率均为q
和p,乙向东、南、西、北四个方向行走的概率均为q
(1)求p和q的值;
(2)设至少经过t分钟,甲、乙两人能首次相遇,试确定t的值,并求t分钟时,甲
乙两人相遇的概率.
17.(本小题满分12分)设向量 =(cos23°,cos67°),
=(cos23°,cos67°),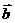 b=(cos68°,cos22°),
b=(cos68°,cos22°),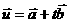 (t∈R).
(t∈R).
(1)求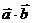 ;
;
(2)求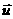 u的模的最小值.
u的模的最小值.
16.设函数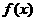 的定义域为
的定义域为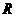 ,若存在常数
,若存在常数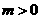 ,使|
,使|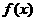 |≤
|≤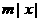 对一切实数
对一切实数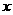 均成立,则称
均成立,则称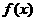 为
为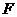 函数。给出下列函数:
函数。给出下列函数:
①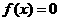 ;
;
②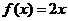 ;
;
③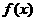 =
=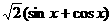 ;
;
④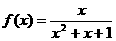 ;
;
⑤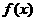 是R上的奇函数,且满足对一切实数
是R上的奇函数,且满足对一切实数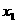 、
、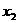 均有
均有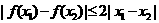 .
.
其中是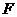 函数的序号为 。
函数的序号为 。
15.若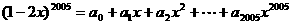 (
(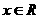 ),则
),则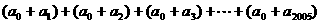 =
(用数字作答)。
=
(用数字作答)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com