
题目列表(包括答案和解析)
4、 递增(减)、摆动、循环数列:
3、 有穷数列与无穷数列:
2、 数列的项与项数:
1、 数列的定义及表示方法:
本章是高考命题的主体内容之一,应切实进行全面、深入地复习,并在此基础上,突出解决下述几个问题:(1)等差、等比数列的证明须用定义证明,值得注意的是,若给出一个数列的前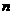 项和
项和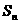 ,则其通项为
,则其通项为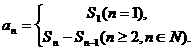 若
若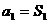 满足
满足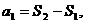 则通项公式可写成
则通项公式可写成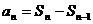 .(2)数列计算是本章的中心内容,利用等差数列和等比数列的通项公式、前
.(2)数列计算是本章的中心内容,利用等差数列和等比数列的通项公式、前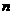 项和公式及其性质熟练地进行计算,是高考命题重点考查的内容.(3)解答有关数列问题时,经常要运用各种数学思想.善于使用各种数学思想解答数列题,是我们复习应达到的目标. ①函数思想:等差等比数列的通项公式求和公式都可以看作是
项和公式及其性质熟练地进行计算,是高考命题重点考查的内容.(3)解答有关数列问题时,经常要运用各种数学思想.善于使用各种数学思想解答数列题,是我们复习应达到的目标. ①函数思想:等差等比数列的通项公式求和公式都可以看作是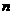 的函数,所以等差等比数列的某些问题可以化为函数问题求解.
的函数,所以等差等比数列的某些问题可以化为函数问题求解.
②分类讨论思想:用等比数列求和公式应分为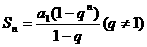 及
及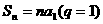 ;已知
;已知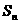 求
求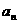 时,也要进行分类;
时,也要进行分类;
③整体思想:在解数列问题时,应注意摆脱呆板使用公式求解的思维定势,运用整
体思想求解.
(4)在解答有关的数列应用题时,要认真地进行分析,将实际问题抽象化,转化为数学问题,再利用有关数列知识和方法来解决.解答此类应用题是数学能力的综合运用,决不是简单地模仿和套用所能完成的.特别注意与年份有关的等比数列的第几项不要弄错.
(1)一元一次不等式:
Ⅰ、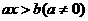 :⑴若
:⑴若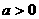 ,则
;⑵若
,则
;⑵若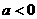 ,则
;
,则
;
Ⅱ、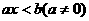 :⑴若
:⑴若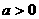 ,则
;⑵若
,则
;⑵若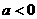 ,则
;
,则
;
(2)一元二次不等式: 一元二次不等式二次项系数小于零的,同解变形为二次项系数大于零;注:要对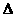 进行讨论:
进行讨论:
(5)绝对值不等式:若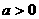 ,则
,则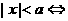 ;
;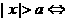 ;
;
注意:(1).几何意义: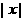 :
;
:
;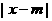 :
;
:
;
(2)解有关绝对值的问题,考虑去绝对值,去绝对值的方法有:
⑴对绝对值内的部分按大于、等于、小于零进行讨论去绝对值;①若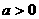 则
则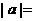 ;②若
;②若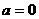 则
则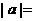 ;③若
;③若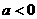 则
则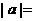 ;
;
(3).通过两边平方去绝对值;需要注意的是不等号两边为非负值。
(4).含有多个绝对值符号的不等式可用“按零点分区间讨论”的方法来解。
(6)分式不等式的解法:通解变形为整式不等式;
⑴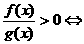 ;⑵
;⑵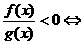 ;
;
⑶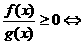 ;⑷
;⑷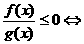 ;
;
(7)不等式组的解法:分别求出不等式组中,每个不等式的解集,然后求其交集,即是这个不等式组的解集,在求交集中,通常把每个不等式的解集画在同一条数轴上,取它们的公共部分。
(8)解含有参数的不等式:
解含参数的不等式时,首先应注意考察是否需要进行分类讨论.如果遇到下述情况则一般需要讨论:
①不等式两端乘除一个含参数的式子时,则需讨论这个式子的正、负、零性.
②在求解过程中,需要使用指数函数、对数函数的单调性时,则需对它们的底数进行讨论.
③在解含有字母的一元二次不等式时,需要考虑相应的二次函数的开口方向,对应的一元二次方程根的状况(有时要分析△),比较两个根的大小,设根为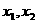 (或更多)但含参数,要分
(或更多)但含参数,要分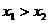 、
、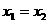 、
、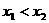 讨论。
讨论。
(1)比较法:作差比较: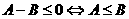
作差比较的步骤:
⑴作差:对要比较大小的两个数(或式)作差。
⑵变形:对差进行因式分解或配方成几个数(或式)的完全平方和。
⑶判断差的符号:结合变形的结果及题设条件判断差的符号。
注意:若两个正数作差比较有困难,可以通过它们的平方差来比较大小。
(2)综合法:由因导果。
(3)分析法:执果索因。基本步骤:要证……只需证……,只需证……
(4)反证法:正难则反。
(5)放缩法:将不等式一侧适当的放大或缩小以达证题目的。
放缩法的方法有:
⑴添加或舍去一些项,如: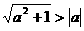 ;
;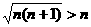
⑵将分子或分母放大(或缩小)
⑶利用基本不等式,如: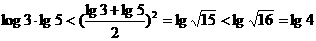 ;
;
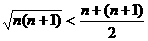
⑷利用常用结论:
Ⅰ、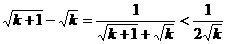 ;
;
Ⅱ、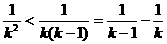 ;
; 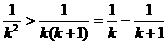 (程度大)
(程度大)
Ⅲ、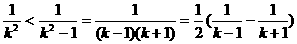 ; (程度小)
; (程度小)
(6)换元法:换元的目的就是减少不等式中变量,以使问题化难为易,化繁为简,常用的换元有三角换元和代数换元。如:
已知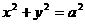 ,可设
,可设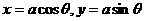 ;
;
已知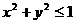 ,可设
,可设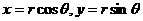 (
(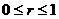 );
);
已知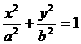 ,可设
,可设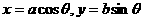 ;
;
已知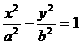 ,可设
,可设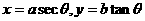 ;
;
(7)构造法:通过构造函数、方程、数列、向量或不等式来证明不等式;
(1)设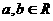 ,则
,则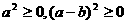 (当且仅当
时取等号)
(当且仅当
时取等号)
(2)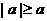 (当且仅当
时取等号);
(当且仅当
时取等号);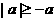 (当且仅当
时取等号)
(当且仅当
时取等号)
(3)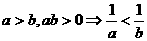 ;
;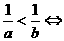 ;
;
注意:上述等号“=”成立的条件;
若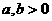 ,则
,则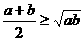 (当且仅当
(当且仅当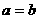 时取等号)
时取等号)
基本变形:①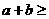 ;
;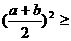 ;
;
②若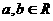 ,则
,则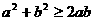 ,
,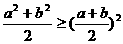
基本应用:①放缩,变形;
②求函数最值:注意:①一正二定三取等;②积定和小,和定积大。
当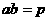 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;
当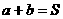 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;
常用的方法为:拆、凑、平方;
如:①函数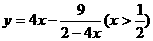 的最小值
。
的最小值
。
②若正数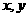 满足
满足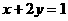 ,则
,则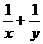 的最小值
。
的最小值
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com