
题目列表(包括答案和解析)
1、等比数列{an}中,a3=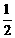 ,a9=8则a5·a6·a7的值为 ( )
,a9=8则a5·a6·a7的值为 ( )
A.64 B.-8 C.8 D.±8
(1)已知集合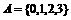 ,
,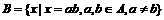 ,则集合B中的元素个数为
,则集合B中的元素个数为
A. 2 B. 3 C. 4 D. 5
(2)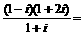
A. 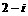 B.
B.
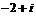 C.
C. 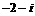 D.
D.
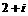
(3)函数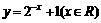 的反函数是
的反函数是
A. 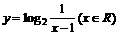 B.
B.
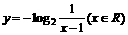
C. 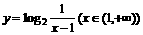 D.
D.
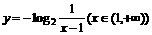
(4)函数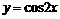 的一个单调递减区间是
的一个单调递减区间是
A. 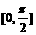 B.
B. 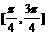 C.
C. 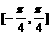 D.
D. 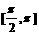
(5)设随机变量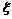 服从二项分布B(n, p),且
服从二项分布B(n, p),且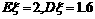 ,则n, p的值分别为
,则n, p的值分别为
A. n=30,p=0.2 B. n=20,p=0.1 C. n=8,p=0.2 D. n=10,p=0.2
(6)等比数列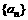 的前n项和为Sn,已知S4=1,S8=3,则
的前n项和为Sn,已知S4=1,S8=3,则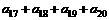 的值为
的值为
A. 4 B. 8 C. 16 D. 32
(7)已知单位向量a、b,它们的夹角为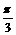 ,则
,则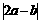 的值为
的值为
A. 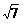 B.
B.
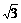 C.
10
D. -10
C.
10
D. -10
(8)已知函数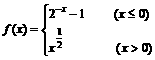 ,若
,若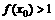 ,则x0的取值范围是
,则x0的取值范围是
A. (-1,1) B. (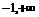 )
)
C. 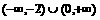 D.
D.
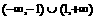
(9)在ΔABC中,角A、B、C所对边分别是a、b、c,且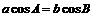 ,则ΔABC的形状是
,则ΔABC的形状是
A. 等腰三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
(10)定义在R上的偶数函数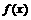 在
在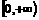 上是增函数,若
上是增函数,若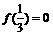 ,则适合不等式
,则适合不等式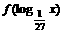 >0的x的取值范围是
>0的x的取值范围是
A. 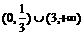 B.
B. 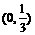 C.
C.
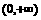 D.
D. 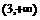
(11)设函数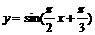 ,若对任意
,若对任意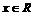 ,存在x1,x2使
,存在x1,x2使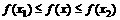 恒成立,则
恒成立,则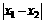 的最小值是
的最小值是
A. 1
B. 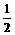 C.
4 D. 2
C.
4 D. 2
(12)甲、乙两工厂2004年元月份的产值相等,甲厂的产值逐月增加且每月增加的数量相同,乙厂产值也逐月增加且每月的增长率相同,若2005年元月份两厂的产值又相等,则2004年7月份两厂的产值关系是
A. 甲厂的产值高 B. 乙厂的产值高
C. 甲厂、乙厂的产值相同 D. 无法确定
泸州市高中2006级第一次诊断考试
数 学(理工农医类)
第Ⅱ卷(非选择题 共90分)
评卷人(13)函数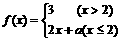 在
在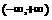 上处处连续,则常数a等于
。、
上处处连续,则常数a等于
。、
(14)已知向量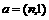 与
与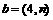 共线,则实数n= 。
共线,则实数n= 。
(15)设数列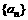 的前n项和Sn满足:
的前n项和Sn满足: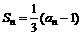 ,则该数列的通项公式an= 。
,则该数列的通项公式an= 。
(16)给出以下命题
①设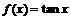 ,则
,则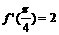 ;②函数
;②函数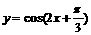 的图象的一条对称轴为
的图象的一条对称轴为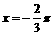 ;③要得到函数
;③要得到函数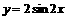 的图象只须将
的图象只须将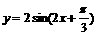 的图象向左平移
的图象向左平移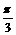 个单位长度。其中正确命题的序号是
。
个单位长度。其中正确命题的序号是
。
(17)(本小题满分12分)
角A、B、C是ΔABC的内角,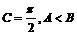 ,向量
,向量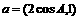 ,
,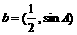 且
且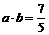 。
。
(1)求sinA的值;
(2)求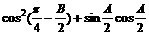 的值。
的值。
已知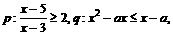 若
若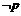 是
是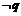 的充分条件,求实数a的范围。
的充分条件,求实数a的范围。
甲、乙两名运动员各自投篮命中率分别为0.6和0.7。
(1)如果每人投篮两次,求甲投进两次,乙投进一次的概率;
(2)如果每人投篮一次,若投进一球得2分,未投进得0分,求两人得分之和的分布列和期望。
评卷人已知函数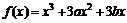 在x=2时有极值,其图象在点(1,f(1))处的切线与直线
在x=2时有极值,其图象在点(1,f(1))处的切线与直线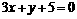 平行。
平行。
(1)求该函数的单调递减区间;
(2)当m>0时,求函数f(x)在[0,m]上的最小值。
评卷人设等差数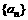 的前n项和为Sn,公差d >0,若
的前n项和为Sn,公差d >0,若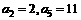 。
。
(1)求数列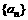 的通项公式;
的通项公式;
(2)设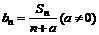 ,若
,若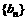 是等差数列且
是等差数列且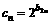 ,求实数a与
,求实数a与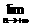
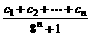 的值。
的值。
已知二次函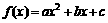 。
。
(1)若任意x1,x2∈R,且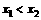 ,都有
,都有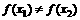 ,求证:关于x的方程
,求证:关于x的方程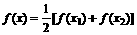 有两个不相等的实数根且必有一个根属于(
有两个不相等的实数根且必有一个根属于(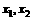 );
);
(2)若关于x的方程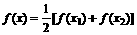 在(
在(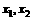 )的根为m,且
)的根为m,且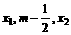 成等差数列,设函数f (x)的图象的对称轴方程为
成等差数列,设函数f (x)的图象的对称轴方程为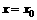 ,求证:
,求证: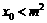 。
。
(1)已知集合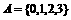 ,
,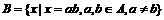 ,则集合B中的元素个数为
,则集合B中的元素个数为
A. 2 B. 3 C. 4 D. 5
(2)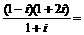
A. 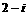 B.
B.
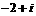 C.
C. 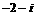 D.
D.
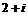
(3)函数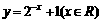 的反函数是
的反函数是
A. 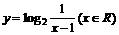 B.
B.
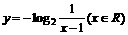
C. 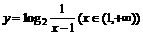 D.
D.
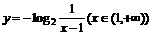
(4)函数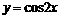 的一个单调递减区间是
的一个单调递减区间是
A. 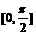 B.
B. 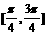 C.
C. 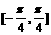 D.
D. 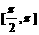
(5)设随机变量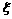 服从二项分布B(n, p),且
服从二项分布B(n, p),且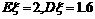 ,则n, p的值分别为
,则n, p的值分别为
A. n=30,p=0.2 B. n=20,p=0.1 C. n=8,p=0.2 D. n=10,p=0.2
(6)等比数列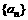 的前n项和为Sn,已知S4=1,S8=3,则
的前n项和为Sn,已知S4=1,S8=3,则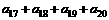 的值为
的值为
A. 4 B. 8 C. 16 D. 32
(7)已知单位向量a、b,它们的夹角为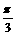 ,则
,则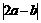 的值为
的值为
A. 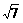 B.
B.
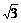 C.
10
D. -10
C.
10
D. -10
(8)已知函数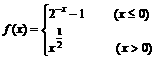 ,若
,若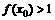 ,则x0的取值范围是
,则x0的取值范围是
A. (-1,1) B. (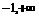 )
)
C. 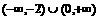 D.
D.
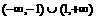
(9)在ΔABC中,角A、B、C所对边分别是a、b、c,且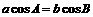 ,则ΔABC的形状是
,则ΔABC的形状是
A. 等腰三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
(10)定义在R上的偶数函数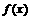 在
在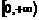 上是增函数,若
上是增函数,若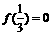 ,则适合不等式
,则适合不等式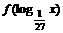 >0的x的取值范围是
>0的x的取值范围是
A. 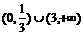 B.
B. 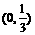 C.
C.
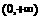 D.
D. 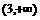
(11)设函数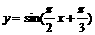 ,若对任意
,若对任意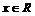 ,存在x1,x2使
,存在x1,x2使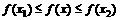 恒成立,则
恒成立,则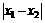 的最小值是
的最小值是
A. 1
B. 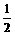 C.
4 D. 2
C.
4 D. 2
(12)甲、乙两工厂2004年元月份的产值相等,甲厂的产值逐月增加且每月增加的数量相同,乙厂产值也逐月增加且每月的增长率相同,若2005年元月份两厂的产值又相等,则2004年7月份两厂的产值关系是
A. 甲厂的产值高 B. 乙厂的产值高
C. 甲厂、乙厂的产值相同 D. 无法确定
泸州市高中2006级第一次诊断考试
数 学(理工农医类)
第Ⅱ卷(非选择题 共90分)
评卷人(13)函数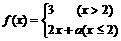 在
在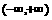 上处处连续,则常数a等于
。、
上处处连续,则常数a等于
。、
(14)已知向量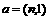 与
与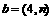 共线,则实数n= 。
共线,则实数n= 。
(15)设数列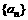 的前n项和Sn满足:
的前n项和Sn满足: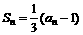 ,则该数列的通项公式an= 。
,则该数列的通项公式an= 。
(16)给出以下命题
①设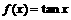 ,则
,则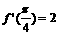 ;②函数
;②函数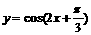 的图象的一条对称轴为
的图象的一条对称轴为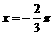 ;③要得到函数
;③要得到函数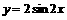 的图象只须将
的图象只须将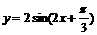 的图象向左平移
的图象向左平移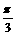 个单位长度。其中正确命题的序号是
。
个单位长度。其中正确命题的序号是
。
(17)(本小题满分12分)
角A、B、C是ΔABC的内角,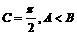 ,向量
,向量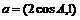 ,
,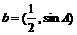 且
且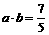 。
。
(1)求sinA的值;
(2)求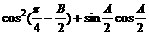 的值。
的值。
已知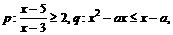 若
若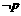 是
是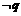 的充分条件,求实数a的范围。
的充分条件,求实数a的范围。
甲、乙两名运动员各自投篮命中率分别为0.6和0.7。
(1)如果每人投篮两次,求甲投进两次,乙投进一次的概率;
(2)如果每人投篮一次,若投进一球得2分,未投进得0分,求两人得分之和的分布列和期望。
评卷人已知函数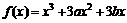 在x=2时有极值,其图象在点(1,f(1))处的切线与直线
在x=2时有极值,其图象在点(1,f(1))处的切线与直线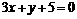 平行。
平行。
(1)求该函数的单调递减区间;
(2)当m>0时,求函数f(x)在[0,m]上的最小值。
评卷人设等差数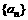 的前n项和为Sn,公差d >0,若
的前n项和为Sn,公差d >0,若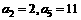 。
。
(1)求数列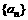 的通项公式;
的通项公式;
(2)设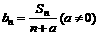 ,若
,若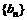 是等差数列且
是等差数列且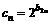 ,求实数a与
,求实数a与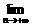
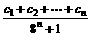 的值。
的值。
已知二次函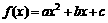 。
。
(1)若任意x1,x2∈R,且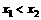 ,都有
,都有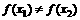 ,求证:关于x的方程
,求证:关于x的方程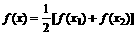 有两个不相等的实数根且必有一个根属于(
有两个不相等的实数根且必有一个根属于(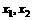 );
);
(2)若关于x的方程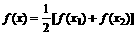 在(
在(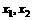 )的根为m,且
)的根为m,且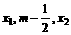 成等差数列,设函数f (x)的图象的对称轴方程为
成等差数列,设函数f (x)的图象的对称轴方程为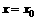 ,求证:
,求证: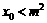 。
。
(1)已知集合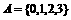 ,
,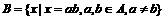 ,则集合B中的元素个数为
,则集合B中的元素个数为
A. 2 B. 3 C. 4 D. 5
(2)与函数y=x相同的是
A. 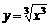 B.
B.
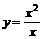 C.
C. 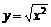 D.
D.
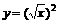
(3)函数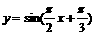 的最小正周期是
的最小正周期是
A.  B.
B. 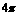 C.4
D. 1
C.4
D. 1
(4)函数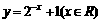 的反函数是
的反函数是
A. 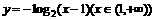 B.
B. 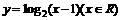
C. 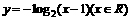 D.
D. 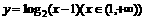
(5)函数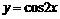 的一个单调递减区间是
的一个单调递减区间是
A. 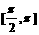 B.
B. 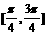 C.
C. 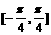 D.
D. 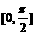
(6)设A(1,2),B(4,2),若点A、B按向量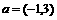 平移后对应点
平移后对应点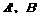 ,则
,则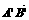 =
=
A. (2,3) B.(3,5) C.(3,0) D. (-4,3)
(7)等比数列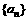 的前n项和为Sn,已知S4=1,S8=3,则
的前n项和为Sn,已知S4=1,S8=3,则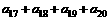 的值为
的值为
A. 32 B. 16 C. 8 D. 4
(8)已知单位向量a、b,它们的夹角为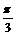 ,则
,则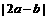 的值为
的值为
A. 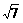 B.
-10 C. 10
D.
B.
-10 C. 10
D. 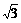
(9)已知函数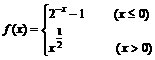 ,若
,若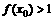 ,则x0的取值范围是
,则x0的取值范围是
A. (-1,1)
B. (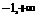 )
)
C. 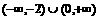 D.
D.
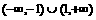
(10)在ΔABC中,角A、B、C所对边分别是a、b、c,且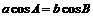 ,则ΔABC的形状是
,则ΔABC的形状是
A. 等腰三角形或直角三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形
(11)定义在R上的偶数函数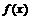 在
在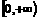 上是增函数,若
上是增函数,若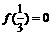 ,则适合不等式
,则适合不等式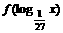 >0的x的取值范围是
>0的x的取值范围是
A. 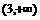 B.
B.
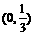 C.
C.
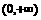 D.
D. 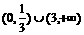
(12)甲、乙两工厂2004年元月份的产值相等,甲厂的产值逐月增加且每月增加的数量相同,乙厂产值也逐月增加且每月的增长率相同,若2005年元月份两厂的产值又相等,则2004年7月份两厂的产值关系是
A. 甲厂的产值高 B. 乙厂的产值高
C. 甲厂、乙厂的产值相同 D. 无法确定
泸州市高中2006级第一次诊断考试
数 学(文史财经类)
第Ⅱ卷(非选择题 共90分)
评卷人(13)一个容量为20的样本,数据的分组及各组的频数如下:
(10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2。
则样本在区间(10,50]上的频率为 。
(14)已知向量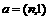 与
与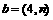 共线,则实数n=
。
共线,则实数n=
。
(15)设数列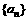 的前n项和Sn满足:
的前n项和Sn满足: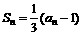 ,则该数列的通项公式an= 。
,则该数列的通项公式an= 。
(16)给出以下命题
①设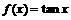 ,则
,则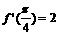 ;②函数
;②函数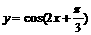 的图象的一条对称轴为
的图象的一条对称轴为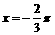 ;③要得到函数
;③要得到函数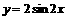 的图象只须将
的图象只须将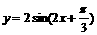 的图象向左平移
的图象向左平移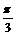 个单位长度。其中正确命题的序号是
。
个单位长度。其中正确命题的序号是
。
(17)(本小题满分12分)
若A是锐角,向量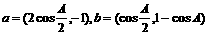 且
且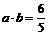 。
。
求tan2A的值。
评卷人已知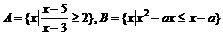 ,若
,若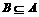 ,求实数a的范围。
,求实数a的范围。
函数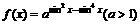 在[0,2
在[0,2 ]上的最大值为
]上的最大值为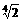 ,求实数a的值与函数f(x)取得最大值时的x集合。
,求实数a的值与函数f(x)取得最大值时的x集合。
2005年10月27日第十届全国人大常委第十八次会议通过了关于修改《中华人民共和国个人所得税法》的决定,修改后的《中华人民共和国个人所得税法》规定“个人工资、薪金等所得,以每月收入额减除费用一千六百元后的余额,为应纳税所得额。”修改后的个人所得率税率表为:
|
级数 |
全月应纳税所得额 |
税率% |
|
1 |
不超过500元的 |
5 |
|
2 |
超过500元至2000元的部份 |
10 |
|
3 |
超过2000元至5000元的部份 |
15 |
|
4 |
超过5000元至20000元的部份 |
20 |
|
… |
|
… |
(1)设个人的月工资、薪金等所得为x元(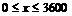 ),月纳税额为y元,写出y与x的函数关系式;
),月纳税额为y元,写出y与x的函数关系式;
(2)若某职员某月工资、薪金等所得为3300元,求该职员该月应纳税多少元?
评卷人已知函数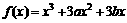 在x=2时有极值,其图象在点(1,f(1))处的切线与直线
在x=2时有极值,其图象在点(1,f(1))处的切线与直线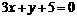 平行。
平行。
(1)求该函数的单调递减区间;
(2)当m>0时,求函数f(x)在[0,m]上的最小值。
评卷人设等差数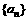 的前n项和为Sn,公差d >0,若
的前n项和为Sn,公差d >0,若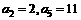 。
。
(1)求数列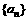 的通项公式;
的通项公式;
(2)设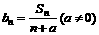 ,若
,若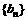 是等差数列,求实数a的值;
是等差数列,求实数a的值;
(3)在(1)(2)下,设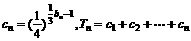 。是否存在正整数m、n,使
。是否存在正整数m、n,使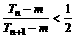 成立,若存在,求出m、n的值;若不存在,说明理由。
成立,若存在,求出m、n的值;若不存在,说明理由。
(1)已知集合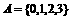 ,
,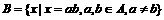 ,则集合B中的元素个数为
,则集合B中的元素个数为
A. 2 B. 3 C. 4 D. 5
(2)与函数y=x相同的是
A. 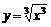 B.
B.
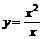 C.
C. 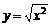 D.
D.
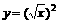
(3)函数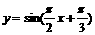 的最小正周期是
的最小正周期是
A.  B.
B. 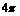 C.4
D. 1
C.4
D. 1
(4)函数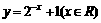 的反函数是
的反函数是
A. 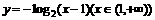 B.
B. 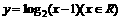
C. 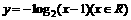 D.
D. 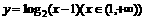
(5)函数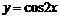 的一个单调递减区间是
的一个单调递减区间是
A. 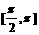 B.
B. 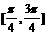 C.
C. 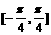 D.
D. 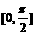
(6)设A(1,2),B(4,2),若点A、B按向量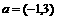 平移后对应点
平移后对应点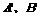 ,则
,则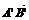 =
=
A. (2,3) B.(3,5) C.(3,0) D. (-4,3)
(7)等比数列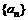 的前n项和为Sn,已知S4=1,S8=3,则
的前n项和为Sn,已知S4=1,S8=3,则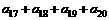 的值为
的值为
A. 32 B. 16 C. 8 D. 4
(8)已知单位向量a、b,它们的夹角为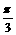 ,则
,则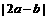 的值为
的值为
A. 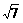 B.
-10 C. 10
D.
B.
-10 C. 10
D. 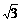
(9)已知函数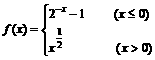 ,若
,若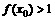 ,则x0的取值范围是
,则x0的取值范围是
A. (-1,1)
B. (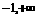 )
)
C. 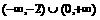 D.
D.
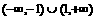
(10)在ΔABC中,角A、B、C所对边分别是a、b、c,且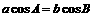 ,则ΔABC的形状是
,则ΔABC的形状是
A. 等腰三角形或直角三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形
(11)定义在R上的偶数函数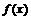 在
在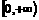 上是增函数,若
上是增函数,若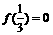 ,则适合不等式
,则适合不等式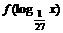 >0的x的取值范围是
>0的x的取值范围是
A.  B.
B.
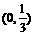 C.
C.
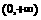 D.
D. 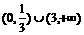
(12)甲、乙两工厂2004年元月份的产值相等,甲厂的产值逐月增加且每月增加的数量相同,乙厂产值也逐月增加且每月的增长率相同,若2005年元月份两厂的产值又相等,则2004年7月份两厂的产值关系是
A. 甲厂的产值高 B. 乙厂的产值高
C. 甲厂、乙厂的产值相同 D. 无法确定
泸州市高中2006级第一次诊断考试
数 学(文史财经类)
第Ⅱ卷(非选择题 共90分)
评卷人(13)一个容量为20的样本,数据的分组及各组的频数如下:
(10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2。
则样本在区间(10,50]上的频率为 。
(14)已知向量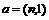 与
与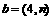 共线,则实数n= 。
共线,则实数n= 。
(15)设数列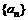 的前n项和Sn满足:
的前n项和Sn满足: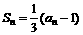 ,则该数列的通项公式an= 。
,则该数列的通项公式an= 。
(16)给出以下命题
①设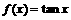 ,则
,则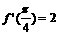 ;②函数
;②函数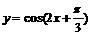 的图象的一条对称轴为
的图象的一条对称轴为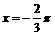 ;③要得到函数
;③要得到函数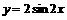 的图象只须将
的图象只须将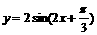 的图象向左平移
的图象向左平移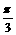 个单位长度。其中正确命题的序号是
。
个单位长度。其中正确命题的序号是
。
(17)(本小题满分12分)
若A是锐角,向量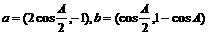 且
且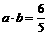 。
。
求tan2A的值。
评卷人已知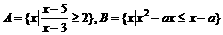 ,若
,若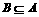 ,求实数a的范围。
,求实数a的范围。
函数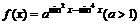 在[0,2
在[0,2 ]上的最大值为
]上的最大值为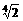 ,求实数a的值与函数f(x)取得最大值时的x集合。
,求实数a的值与函数f(x)取得最大值时的x集合。
2005年10月27日第十届全国人大常委第十八次会议通过了关于修改《中华人民共和国个人所得税法》的决定,修改后的《中华人民共和国个人所得税法》规定“个人工资、薪金等所得,以每月收入额减除费用一千六百元后的余额,为应纳税所得额。”修改后的个人所得率税率表为:
|
级数 |
全月应纳税所得额 |
税率% |
|
1 |
不超过500元的 |
5 |
|
2 |
超过500元至2000元的部份 |
10 |
|
3 |
超过2000元至5000元的部份 |
15 |
|
4 |
超过5000元至20000元的部份 |
20 |
|
… |
|
… |
(1)设个人的月工资、薪金等所得为x元(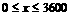 ),月纳税额为y元,写出y与x的函数关系式;
),月纳税额为y元,写出y与x的函数关系式;
(2)若某职员某月工资、薪金等所得为3300元,求该职员该月应纳税多少元?
评卷人已知函数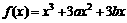 在x=2时有极值,其图象在点(1,f(1))处的切线与直线
在x=2时有极值,其图象在点(1,f(1))处的切线与直线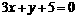 平行。
平行。
(1)求该函数的单调递减区间;
(2)当m>0时,求函数f(x)在[0,m]上的最小值。
评卷人设等差数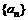 的前n项和为Sn,公差d >0,若
的前n项和为Sn,公差d >0,若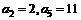 。
。
(1)求数列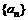 的通项公式;
的通项公式;
(2)设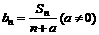 ,若
,若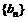 是等差数列,求实数a的值;
是等差数列,求实数a的值;
(3)在(1)(2)下,设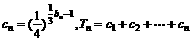 。是否存在正整数m、n,使
。是否存在正整数m、n,使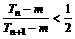 成立,若存在,求出m、n的值;若不存在,说明理由。
成立,若存在,求出m、n的值;若不存在,说明理由。
22.(本小满分14分)
设等差数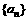 的前n项和为Sn,公差d >0,若
的前n项和为Sn,公差d >0,若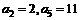 。
。
(1)求数列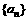 的通项公式;
的通项公式;
(2)设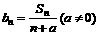 ,若
,若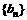 是等差数列,求实数a的值;
是等差数列,求实数a的值;
(3)在(1)(2)下,设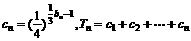 。是否存在正整数m、n,使
。是否存在正整数m、n,使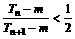 成立,若存在,求出m、n的值;若不存在,说明理由。
成立,若存在,求出m、n的值;若不存在,说明理由。
21.(本小题满分12分)
已知函数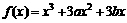 在x=2时有极值,其图象在点(1,f(1))处的切线与直线
在x=2时有极值,其图象在点(1,f(1))处的切线与直线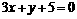 平行。
平行。
(1)求该函数的单调递减区间;
(2)当m>0时,求函数f(x)在[0,m]上的最小值。
20.(本小题12分)
2005年10月27日第十届全国人大常委第十八次会议通过了关于修改《中华人民共和国个人所得税法》的决定,修改后的《中华人民共和国个人所得税法》规定“个人工资、薪金等所得,以每月收入额减除费用一千六百元后的余额,为应纳税所得额。”修改后的个人所得率税率表为:
|
级数 |
全月应纳税所得额 |
税率% |
|
1 |
不超过500元的 |
5 |
|
2 |
超过500元至2000元的部份 |
10 |
|
3 |
超过2000元至5000元的部份 |
15 |
|
4 |
超过5000元至20000元的部份 |
20 |
|
… |
|
… |
(1)设个人的月工资、薪金等所得为x元(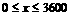 ),月纳税额为y元,写出y与x的函数关系式;
),月纳税额为y元,写出y与x的函数关系式;
(2)若某职员某月工资、薪金等所得为3300元,求该职员该月应纳税多少元?
19.(本小题满分12分)
函数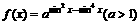 在[0,2
在[0,2 ]上的最大值为
]上的最大值为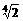 ,求实数a的值与函数f(x)取得最大值时的x集合。
,求实数a的值与函数f(x)取得最大值时的x集合。
18.(本小题满分12分)
已知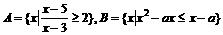 ,若
,若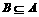 ,求实数a的范围。
,求实数a的范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com