
题目列表(包括答案和解析)
20、(本小题满分14分) 已知函数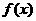 的定义域为
的定义域为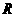 ,对任意实数
,对任意实数 、
、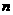 ,满足
,满足
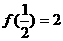 ,且
,且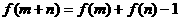 ,当
,当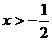 时,
时,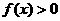
(1)求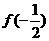 的值;
的值;
(2)求证: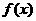 在定义域
在定义域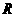 上是单调递增函数。
上是单调递增函数。
解:(1)令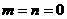 ,得
,得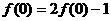 ,
,
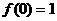
又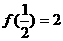 ,令
,令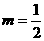 ,
,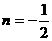 ,得
,得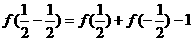

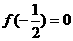
(2)设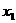 ,
,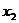
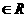 且
且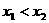 ,则
,则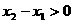 ,
,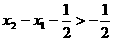
当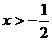 时,
时,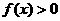

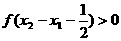
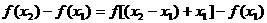
=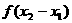 +
+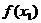 -1-
-1-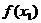
=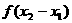 -1
-1
=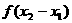 +
+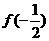 -1
-1
=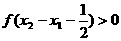
因此,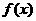 是增函数。
是增函数。
19、(本小题满分14分) 二次函数f(x)满足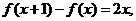 且f(0)=1.
且f(0)=1.
(1) 求f(x)的解析式;
(2) 在区间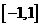 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
解: (1)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,所以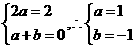 ,∴f(x)=x2-x+1.
,∴f(x)=x2-x+1.
(2)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1,1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x=,所以g(x) 在[-1,1]上递减.
故只需g(1)>0,即12-3×1+1-m>0,解得m<-1.
18、(本题满分14分) 已知:命题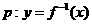 是
是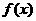 =
=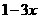 的反函数且
的反函数且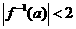 ,命题q:集合
,命题q:集合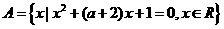 ,
,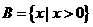 且
且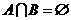 ,求实数a的取值范围,使p、q中有且只有一个为真命题。
,求实数a的取值范围,使p、q中有且只有一个为真命题。
解
: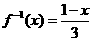 由
由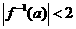 得:
得:
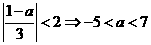
设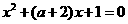 判别式为
判别式为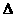
当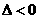 时,
时,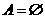 ,此时
,此时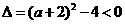 ,
,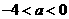
当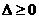 时,由
时,由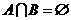 得
得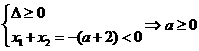
 a>-4
a>-4
(1)若p真q假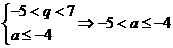
(2)若p假q真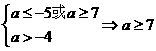 ---------------------2
---------------------2
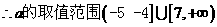
17、(本题满分14分)某种商品在近30天内,每件的销售价格P(元)与时间 t (天)的函数关系近似地满足P=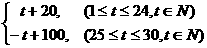 ,商品的日销售量Q(件)与时间t (天)的函数关系近似地满足Q=
,商品的日销售量Q(件)与时间t (天)的函数关系近似地满足Q=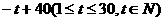 。求这种商品日销售金额R的最大值,并指出销售金额最大的一天是30天中的第几天。
。求这种商品日销售金额R的最大值,并指出销售金额最大的一天是30天中的第几天。
解: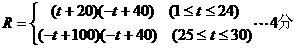
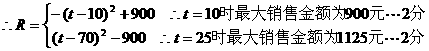
所以这种商品日销售金额R的最大值为1125元,销售金额最大的一天是30天中的第25天。
16、(本题满分12分)已知f(x)=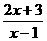 。
。
(1)解不等式:f(x)>1
(2) 当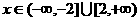 时,求f(x)的值域。
时,求f(x)的值域。
解:(1) 由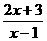 >1得,
>1得,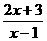 -
-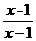 >0, (2’)
>0, (2’)
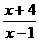 >0 (3’)
>0 (3’)
(x+4)(x-1)>0 x< -4或x>1 (5’) 故解集为 (6’)
(6’)
(2)由y=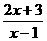 得,x=
得,x=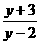 故
故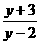 ≤-2或
≤-2或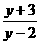 ≥2 (4’)
≥2 (4’)
解上述不等式得: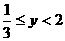 或2<y≤7 (6’)
或2<y≤7 (6’)
故值域为{y|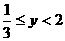 或2<y≤7}
或2<y≤7}
15、(本题满分12分)若a∈R, A=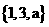 , B=
, B=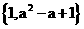 , A∪B=A , 求a的值。
, A∪B=A , 求a的值。
解: ………3分
………3分
 ………7分
………7分
得: 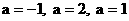 ……………11分
……………11分
经检验: 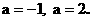 ……………13分
……………13分
13、
0
14 、
( -2 , 0 )∪
11、 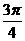 12、
(2 ,3)∪ (3, + ∞)
12、
(2 ,3)∪ (3, + ∞)
20、(本小题满分14分) 已知函数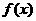 的定义域为
的定义域为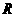 ,对任意实数
,对任意实数 、
、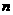 ,满足
,满足
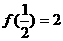 ,且
,且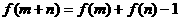 ,当
,当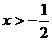 时,
时,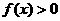
(1)求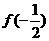 的值;
的值;
(2)求证: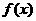 在定义域
在定义域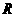 上是单调递增函数。
上是单调递增函数。

 2005~2006学年度第一学期期中考试
2005~2006学年度第一学期期中考试
高 三 数 学 试 卷(第二卷)
19、(本小题满分14分) 二次函数f(x)满足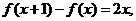 且f(0)=1.
且f(0)=1.
(1) 求f(x)的解析式;
(2) 在区间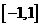 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com