
题目列表(包括答案和解析)
(13)3
(14)-84
(15)②,③
(16)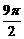
提示:
13.由题意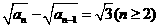 ,
, 是首项为
是首项为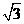 ,公差为
,公差为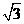 的等差数列.
的等差数列.
9.等比数列求和.
8. .
.
(1)B (2)B (3)D (4)D (5)B (6)B
(7)A (8)C (9)C (10)B (11)C (12)C
提示:
4.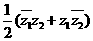 =
=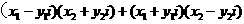 =
=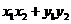 =
=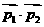 .
.
22.(本小题满分14分)
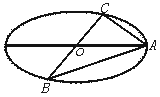
已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆
中心O,如图,且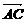 ·
·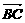 =0,|BC|=2|AC|,
=0,|BC|=2|AC|,
(1)求椭圆的方程;
(2)如果椭圆上两点P、Q使∠PCQ的平分线垂直AO,则总存在实数λ,使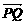 =λ
=λ ,
,
 请给出证明.0
请给出证明.0
高三数学(三)参考解答及评分标准
21.(本小题满分12分)
已知函数f(x)=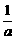 (3x-b)的图象过点A(1,2),B(2,5)
(3x-b)的图象过点A(1,2),B(2,5)
(1)求函数f-1(x)的解析式;
(2)记an=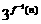 ,n∈N*,是否存在正数k,使得(1+
,n∈N*,是否存在正数k,使得(1+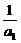 )(1+
)(1+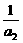 )…(1+
)…(1+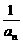 )≥k
)≥k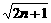 对
对
一切n∈N*均成立,若存在求出k的最大值,若不存在说明理由。
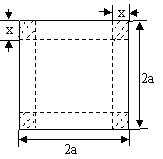
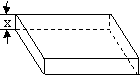
20.(本题满分12分)从边长2a的正方形铁片的四个角各截一个边长为x的正方形,然后拆
成一个无盖的长方体盒子,要求长方体的高度x与底面正方形边长的比不超过正常数t.
(1)把铁盒的容积V表示为x的函数,并指出其定义域;
(2)x为何值时,容积V有最大值.
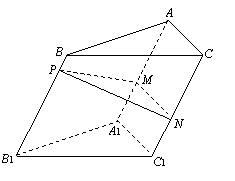
19.(本题满分12分) 如图,点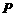 为斜三棱柱
为斜三棱柱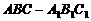 的侧棱
的侧棱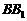 上一点,
上一点,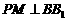
交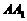 于点
于点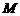 ,
,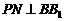 交
交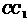 于点
于点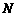 .
.
(1)求证: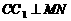 ;
;
(2)在任意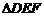 中有余弦定理:
中有余弦定理: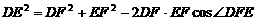 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
18.(本小题满分12分)
口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标
有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,
记第一次与第二次取到卡片上数字之和为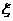 .
.
(1)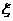 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;
(2)求随机变量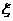 的期望E
的期望E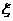 .
.
17.(本小题满分12分)
已知 、
、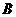 是
是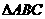 的两个内角,且
的两个内角,且 、
、 是方程
是方程 的两个实根,求
的两个实根,求 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com