
题目列表(包括答案和解析)
7.设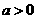 ,对于函数
,对于函数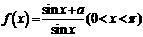 ,下列结论正确的是( )
,下列结论正确的是( )
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
6.函数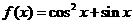 在区间
在区间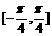 上的最小值是(
)
上的最小值是(
)
A.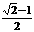 B.
B.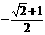 C.-1 D.
C.-1 D.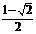
5. 已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是( )
A. 1 B. -1 C. 2k+1 D. -2k+1
4.当-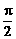 ≤x≤
≤x≤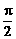 时, 函数f (x)=sinx+
时, 函数f (x)=sinx+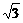 cosx的( )。
cosx的( )。
A.最大值是2,最小值是-2 B.最大值是1,最小值是-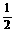
C.最大值是1,最小值是-1 D.最大值是2,最小值是-1
3.函数y=sinxcosx+sinx+cosx的最大值是 .
2.函数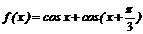 的最小值是
.
的最小值是
.
1.函数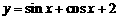 的最小值是 .
的最小值是 .
例15、是否存在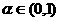 ,使得一个无穷正数列
,使得一个无穷正数列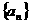 满足1+
满足1+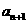 ≤
≤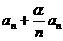 .
.
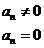 例16、对给定的
例16、对给定的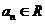 ,定义
,定义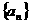 满足
满足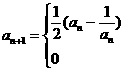
证明这个数列中有无穷多个非正项.
(1)选代方法
例4、(1)设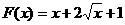 ,计算
,计算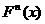 .
.
(2)设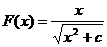 ,计算
,计算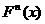 .
.
(3)设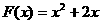 ,计算
,计算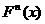 .
.
(4)设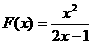 ,计算
,计算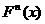 .
.
例5、设数列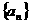 ,满足
,满足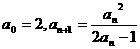 (
(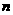 =0,1,2……),求通项公式和
=0,1,2……),求通项公式和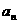 的极限.
的极限.
例6、设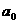 =1,
=1,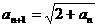 ,求证:
,求证: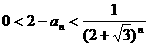
例7、已知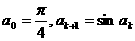 ,求证:
,求证: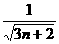 ≤
≤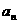 ≤
≤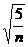
例8、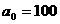 ,
,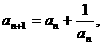 求证:
求证: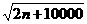 ≤
≤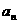 ≤
≤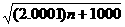
(2)待定系数
例9、已知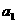 ,
,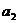 ,
,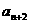 =
=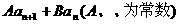 ,求
,求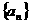 通项公式.
通项公式.
例10、已知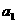 及
及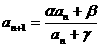 (其中
(其中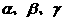 ,为常数,且
,为常数,且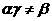 ),求
),求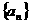 的通项.
的通项.
(3)周期数列
|
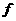 定义在整数集上,且满足
定义在整数集上,且满足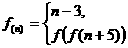
求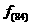 .
.
例12、定义数列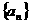 ,
,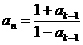 (
(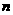 ≥2,
≥2,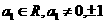 )判断数列
)判断数列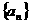 的周期性.
的周期性.
例13、设数列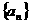 满足:
满足: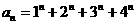 ,其中
,其中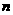 =1,2,3,……,问怎样的自然数
=1,2,3,……,问怎样的自然数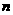 ,
,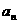 可被10整除.
可被10整除.
例14、求证:和式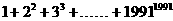 不能表示成
不能表示成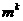 的形式,其中
的形式,其中 与
与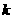 均是自然数,且
均是自然数,且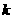 ≥2.
≥2.
例1、设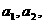
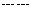
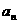 ∈R+,
∈R+,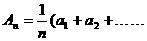
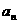 ),
),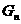 =
=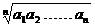
求证: ≥
≥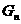 (当且仅当
(当且仅当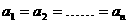 时成立)
时成立)
例2、数列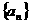 满足
满足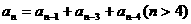 ,其前几项为1,1,2,4,6,……,数列
,其前几项为1,1,2,4,6,……,数列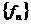 定义为
定义为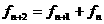 ,且
,且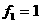 ,
,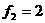 ,求证:
,求证: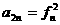 ,
,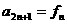 ·
·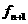
例3、m、n是正整数,求证:不定方程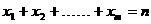 的非负整解的组数为
的非负整解的组数为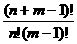
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com