
题目列表(包括答案和解析)
1.能够运用归纳、猜想、分析、化归等方法探索出命题条件,然后给予证明;
2.培养学生空间想象能力,并能把空间想象能力与运算能力,逻辑思维能力相结合.
[例题讲解]
 例题1
例题1
(1) 如图: 平面
平面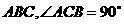 且
且
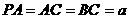 , 则异面直线
, 则异面直线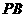 与
与
 所成角的正切值等于________;
所成角的正切值等于________;
(2) 下面是关于三棱锥的四个命题:
①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥;
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥;
④侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥,其中,真命题的编号是___________.(写出的所有真命题的编号).
(3)四棱锥 中,
中,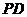
 底面
底面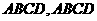 为正方形,且
为正方形,且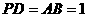 ,
, 为
为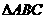 的重心,则
的重心,则 与底面ABCD所成的角为
( )
与底面ABCD所成的角为
( )
A  B
B  C
C 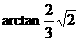 D
D 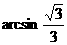
(4)已知球的表面积为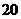
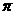 ,球面上有
,球面上有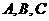 三点,如果
三点,如果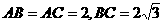 ,则球心到平面ABC的距离为
( )
,则球心到平面ABC的距离为
( )
A 1 B 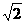 C
C 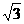 D 2
D 2
(5) 垂直于正六边形
垂直于正六边形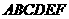 所在平面,若正六边形边长为
所在平面,若正六边形边长为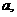 且PD=
且PD=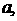 则点
则点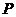
到BC的距离为 ( )
A  B
B 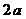 C
C 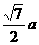 D
D 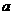
例2
在棱长为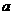 的正方体
的正方体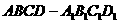 中,
中,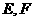 分别是
分别是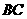 ,
,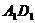 的中点
的中点
(1)求证:四边形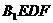 是菱形;
是菱形;
(2)求直线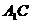 与DE所成的角;
与DE所成的角;
(3)求直线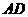 与平面
与平面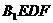 所成的角;
所成的角;
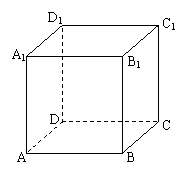 (4)求面
(4)求面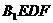 与面
与面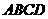 所成的角.
所成的角.
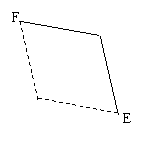
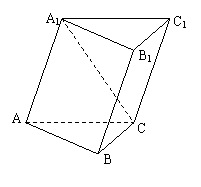
例3若斜三棱柱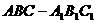 的侧面
的侧面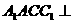 底面
底面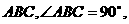
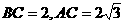 ,且
,且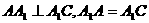
(1)求侧棱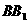 到侧面
到侧面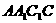 的距离;
的距离;
(2)求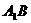 与平面
与平面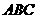 所成的角;
所成的角;
(3)求侧棱 到侧面
到侧面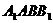 的距离;
的距离;
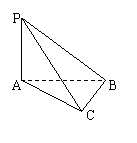
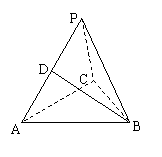
例4 在三棱锥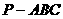 中,
中,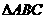 是正三角形,
是正三角形,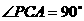 ,
,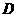 为
为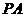 的中点,
的中点,
二面角 为
为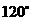 ,
,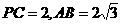 .
.
(1)求证: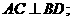
(2)求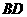 与底面ABC所成的角;
与底面ABC所成的角;
(3)求三棱锥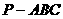 的体积.
的体积.
高三数学第二轮复习教学案
第十三课时 立体几何的探索性问题
班级 学号 姓名
[考纲解读]
考查学生归纳、判断等各方面的能力,培养学生的创新意识.
[教学目标]
1.能够运用转化的思想化空间角为平面角;化线面间距离,面面间距离等为点到线或 线到面的距离.
2.掌握两条异面直线间的距离(只要求会计算已给出公垂线时的距离)直线和平面间的距离及两个平面间的距离的概念,并会求直线和平面间的距离,两个平面间的距离.
[教学目标]
1.掌握两条直线所成的角、直线和平面所成的角及二面角的平面角的概念,并会求
这些角.
2. 进一步发挥解几问题中几何方法与代数方法的互补作用.
[例题讲解]
例题1
(1)若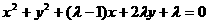 表示圆,则
表示圆,则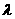 的取值范围为( )
的取值范围为( )
A 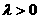 B
B 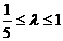 C
C 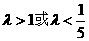 D
D 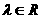
(2)设P是椭圆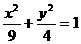 上一动点,
上一动点,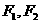 是椭圆的两个焦点,则
是椭圆的两个焦点,则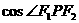 的最小值是( )
的最小值是( )
A 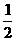 B
B 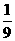 C
C 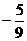 D
D
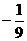
(3)已知双曲线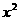
 ,则过P(2,1)且与双曲线有且只有一个公共点的直线有( )条
,则过P(2,1)且与双曲线有且只有一个公共点的直线有( )条
A 1 B 2 C 3 D 4
(4)设双曲线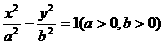 中,离心率
中,离心率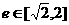 ,则两条渐近线的夹角
,则两条渐近线的夹角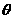 的取值范围是_________.
的取值范围是_________.
(5)抛物线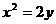 上离点
上离点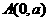 最近的点恰好是顶点,则
最近的点恰好是顶点,则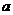 的取值范围是______.
的取值范围是______.
(6)点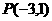 在椭圆
在椭圆 的左准线上,过点P且方向为
的左准线上,过点P且方向为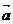
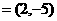 的光线经直线
的光线经直线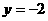 反射后通过椭圆的左焦点,则这个椭圆的离心率为__________.
反射后通过椭圆的左焦点,则这个椭圆的离心率为__________.
例2设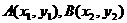 两点在抛物线
两点在抛物线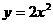 上,
上,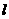 是AB的垂直平分线,当直线
是AB的垂直平分线,当直线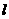 的斜率为2时,求
的斜率为2时,求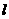 在
在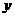 轴上截距的取值范围.
轴上截距的取值范围.
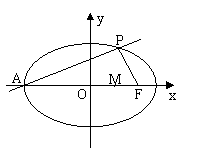
例3如图,点A、B分别是椭圆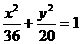 的长轴的左右端点,点
的长轴的左右端点,点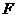 是椭圆的右焦点,点
是椭圆的右焦点,点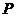 在椭圆上,且位于
在椭圆上,且位于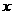 轴上方,
轴上方,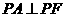 .
.
(1) 求点P的坐标.
(2)设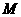 是椭圆长轴
是椭圆长轴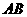 上一点,
上一点,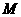 到直线
到直线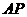 的距离等于
的距离等于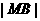 ,求椭圆上点到点
,求椭圆上点到点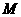 的距离
的距离 的最小值.
的最小值.
例4已知双曲线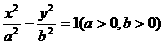 的右焦点为
的右焦点为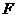 ,过点
,过点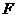 作直线
作直线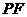 垂直于该双曲线的一条渐近线
垂直于该双曲线的一条渐近线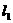 于P
于P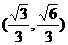
(1)求该双曲线的方程.
(2)过点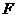 作直线
作直线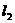 交该双曲线于
交该双曲线于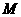 、
、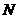 两点,如果
两点,如果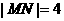 ,求直线
,求直线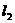 的方程.
的方程.
例5给定抛物线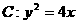 ,
,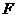 是
是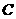 的焦点,过点
的焦点,过点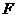 的直线
的直线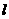 与
与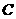 相交于A,B两点,设
相交于A,B两点,设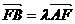 ,若
,若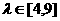 ,求
,求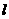 在
在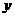 轴上的截距的变化范围.
轴上的截距的变化范围.
1. 夯实基础知识,灵活运用基本方法解决问题.
2.理解能用函数、方程、不等式等方法研究曲线的性质.
[教学目标]
1.通过方程研究性质是解析几何的一个基本问题.
2.进一步培养学生逻辑推理能力、运算能力、分析问题和解决问题的能力.
[例题讲解]
例题1
(1)圆心在抛物线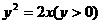 上,并且与抛物线的准线及
上,并且与抛物线的准线及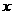 轴都相切的圆的方程是( )
轴都相切的圆的方程是( )
A 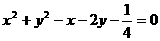 B
B 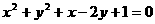
C 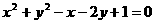 D
D 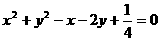
(2)已知椭圆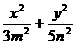 =1和双曲线
=1和双曲线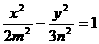 有公共的焦点,那么双曲线的渐近线方程是( )
有公共的焦点,那么双曲线的渐近线方程是( )
A  B
B 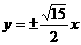 C
C 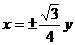 D
D 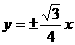
(3)已知两点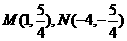 给出下列曲线方程:①
给出下列曲线方程:①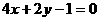 ;②
;②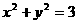 ;③
;③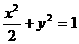 ;④
;④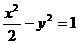 ,在曲线上存在点P满足
,在曲线上存在点P满足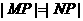 的所有曲线方程是( )
的所有曲线方程是( )
A ①③ B ②④ C ①②③ D ②③④
(4)已知两点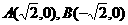 ,动点
,动点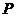 在
在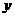 轴上的射影为
轴上的射影为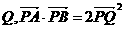 ,则动点P的轨迹方程为_________.
,则动点P的轨迹方程为_________.
(5)已知直线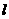 交椭圆
交椭圆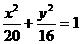 于
于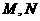 两点,椭圆与
两点,椭圆与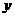 轴的正半轴交于B点,若
轴的正半轴交于B点,若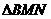 的重心恰好落在椭圆的右焦点上,则直线
的重心恰好落在椭圆的右焦点上,则直线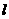 的方程是_________.
的方程是_________.
(6)已知曲线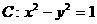 及直线
及直线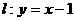 ,曲线
,曲线 与
与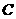 关于直线
关于直线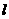 对称,则曲线
对称,则曲线 的方程为________.
的方程为________.
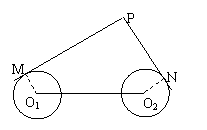 例2如图,圆
例2如图,圆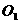 和圆
和圆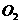 的半径都等于1,
的半径都等于1,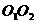 =4,过动点P分别作圆
=4,过动点P分别作圆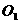 、圆
、圆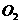 的切线
的切线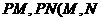 为切点),使得
为切点),使得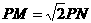 ,试建立平面直角坐标系,并求动点P的轨迹方程.
,试建立平面直角坐标系,并求动点P的轨迹方程.
例3 一个椭圆中心在原点,焦点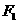 、
、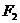 在
在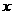 轴上,P(
轴上,P(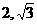 )是椭圆上一点,且
)是椭圆上一点,且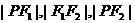 成等差数列,求椭圆的方程.
成等差数列,求椭圆的方程.
例4如图,过点A(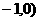 ,斜率为
,斜率为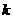 的直线
的直线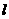 与抛物线
与抛物线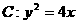 交于P、
交于P、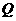 两点,(1)若曲线C的焦点F与P、
两点,(1)若曲线C的焦点F与P、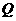 、R三点按如图顺序成平行四边形
、R三点按如图顺序成平行四边形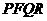 ,求点R
,求点R
的轨迹方程.
(2)设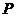 、
、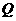 两点只在第一象限运动,点(0,8)与线段
两点只在第一象限运动,点(0,8)与线段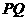 中点的连线交
中点的连线交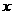 轴于点N,当点N在A点右侧时,求
轴于点N,当点N在A点右侧时,求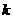 的取值范围.
的取值范围.
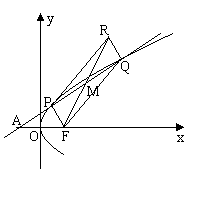
例5点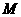 是椭圆
是椭圆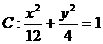 上的一点,
上的一点,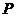 、
、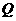 、
、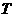 分别为
分别为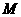 关于
关于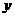 轴、原点、
轴、原点、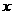 轴的对称点,
轴的对称点,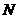 为椭圆
为椭圆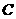 上异于
上异于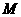 的另一点,且
的另一点,且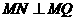 ,
, 与
与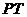 的交点为
的交点为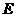 ,当
,当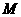 沿椭圆
沿椭圆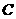 运动时,求动点
运动时,求动点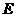 的轨迹方程.
的轨迹方程.
高三数学第二轮复习教学案
第十六课时 定义法与几何法及函数、方程、不等式法研究曲线性质
班级 学号 姓名
[考纲解读]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com