
题目列表(包括答案和解析)
2.在△ABC中,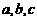 分别为角A,B,C的对边,且
分别为角A,B,C的对边,且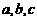 成等比数列.
成等比数列.
(I)求∠B的范围;(II)求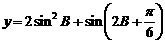 的取值范围.
的取值范围.
22.(本小题满分12分)
已知函数f(x)=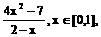
(1)求函数f(x)的单调区间和值域;
(2)设a≥1, 函数g(x)=x3-3a2x-2a, x∈[0,1], 若对于任意x1∈[0,1], 总存在x0∈[0,1], 使得g((x0) =f(x1)成立,求a的取值范围
21.(本小题满分14分)
设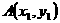 .
.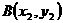 两点在抛物线
两点在抛物线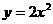 上,
上,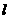 是
是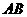 的垂直平分线
的垂直平分线
1)当且仅当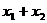 取何值时,直线
取何值时,直线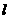 经过抛物线的焦点
经过抛物线的焦点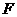 ?证明你的结论;
?证明你的结论;
2)当直线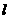 的斜率为2时,求
的斜率为2时,求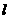 在
在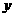 轴上截距的取值范围
轴上截距的取值范围
20.(本小题满分12分)
在等差数列{an}中,公差d≠0,且a2是a1和a4的等比中项,已知a1,a3,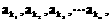 成等比数列,求数列k1,k2,k3,…,kn的通项kn
成等比数列,求数列k1,k2,k3,…,kn的通项kn
19.(本小题满分12分)
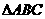 中,内角
中,内角 .
. .
.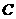 的对边分别为
的对边分别为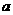 .
.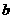 .
.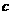 ,已知
,已知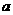 .
.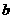 .
.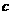 成等比数列,且
成等比数列,且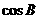
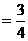

(1)求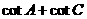 的值;
的值;
(2)若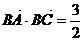 ,求
,求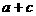 的值
的值
18.(本小题满分12分)
四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,
平面VAD⊥底面ABCD
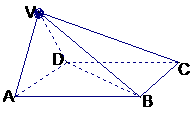 1)求证AB⊥面VAD;
1)求证AB⊥面VAD;
2)求面VAD与面VDB所成的二面角的大小.
17.(本小题满分12分)
甲.乙.丙三台机器是否需要照顾相互之间没有影响 已知在某一个小时内,甲.乙都需要照顾的概率是0.05,甲.丙都需要照顾的概率是0.05,乙.丙都需要照顾的概率是0.125
已知在某一个小时内,甲.乙都需要照顾的概率是0.05,甲.丙都需要照顾的概率是0.05,乙.丙都需要照顾的概率是0.125
1)求甲.乙.丙三台机器在这一个小时内各自需要照顾的概率?
2)计算在这一个小时内至少有一台需要照顾的概率?
16.已知在△ABC中,∠ACB=90°,BC=3,AC=4,P是AB上的点,则P到AC.BC距离的的乘积的最大值是

15.设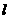 为平面上过点(0,1)的直线,
为平面上过点(0,1)的直线,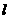 的斜率等可能地取-2
的斜率等可能地取-2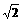 ,-
,-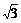 ,-
,-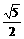 ,0,
,0,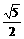 ,
,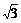 , 2
, 2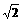 , 用ξ表示坐标原点到
, 用ξ表示坐标原点到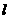 的距离,则随机变量ξ的数学期望Eξ=
的距离,则随机变量ξ的数学期望Eξ=

14.已知向量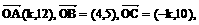 ,且A.B.C三点共线,则k= .
,且A.B.C三点共线,则k= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com