
题目列表(包括答案和解析)
8、(选做题)
设椭圆的中心是坐标原点,长轴在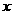 轴上,离心率
轴上,离心率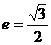 ,已知
,已知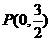 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为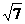 ,求这个椭圆的方程.
,求这个椭圆的方程.
高三数学教学案 第八章 圆锥曲线
第三课时 双曲线(一)
考纲摘录
掌握双曲线的定义,标准方程和双曲线的简单几何性质.
知识概要
双曲线定义的两种形式,标准方程的两种情形,几何量a,b,c,e,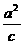 等之间的关系;特征三角形;渐近线等.
等之间的关系;特征三角形;渐近线等.
重点、难点
双曲线的性质及应用,双曲线标准方程的求解方法.
基础练习
7、如图△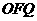 的面积为S,且
的面积为S,且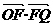 =1.(1)若
=1.(1)若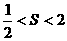 ,求向量
,求向量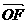 与
与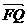 的夹角
的夹角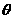 的取值范围,(2)设
的取值范围,(2)设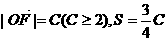 ,若以O为中心,F为焦点的椭圆经过点
,若以O为中心,F为焦点的椭圆经过点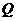 ,当
,当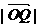 取得最小值时,求此椭圆的方程.
取得最小值时,求此椭圆的方程.
6、如图,在△AFB中,∠AFB=150°,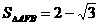 ,一个椭圆以F为一个焦点,以A,B分别作为长、短轴的一个端点,以原点O作为中心,求该椭圆的方程.
,一个椭圆以F为一个焦点,以A,B分别作为长、短轴的一个端点,以原点O作为中心,求该椭圆的方程.
5、一个椭圆的离心率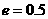 ,准线方程为
,准线方程为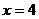 ,对应的焦点为F(2,0),则该椭圆的中心为__________,椭圆的方程为____________________.
,对应的焦点为F(2,0),则该椭圆的中心为__________,椭圆的方程为____________________.
4、椭圆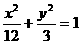 的左、右焦点为
的左、右焦点为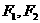 点P在椭圆上,若线段
点P在椭圆上,若线段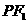 的中点在
的中点在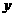 轴上,则
轴上,则 ___________.
___________.
3、椭圆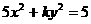 的一个焦点为(0,2),则
的一个焦点为(0,2),则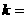 ___________.
___________.
2、设P为椭圆上一点,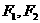 为两焦点,
为两焦点,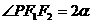 ,
,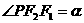 (
(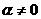 ),那么离心率为( )
),那么离心率为( )
A.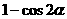 B.
B.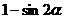 C.
C. D.
D.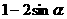
1、若椭圆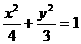 内有一点
内有一点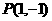 ,F为右焦点,椭圆上有一点M,使|MP|+2|MF|的最小,则M的值为( )
,F为右焦点,椭圆上有一点M,使|MP|+2|MF|的最小,则M的值为( )
A.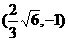 B.
B.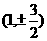 C.
C.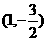 D.
D.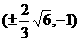
4、若椭圆的两准线之间的距离不大于长轴长的3倍,则它的离心率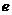 的范围为______________.
的范围为______________.
例题讲解
例1、若椭圆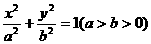 上存在一点M,使
上存在一点M,使 ,求椭圆离心率的范围.
,求椭圆离心率的范围.
例2、已知F是椭圆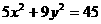 的左焦点,P是椭圆上的动点,A(1,1)是一定点
的左焦点,P是椭圆上的动点,A(1,1)是一定点
(1)求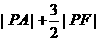 的最小值,并求P的坐标;
的最小值,并求P的坐标;
(2)求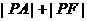 的最大值与最小值.
的最大值与最小值.
例3、已知椭圆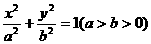 ,长轴的两端点为A、B,如果椭圆上存在一点Q,使∠AQB=120°,求椭圆离心率的取值范围.
,长轴的两端点为A、B,如果椭圆上存在一点Q,使∠AQB=120°,求椭圆离心率的取值范围.
例4、已知椭圆的中心在原点,离心率为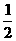 ,一个焦点为F
,一个焦点为F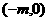 (
( 为大于0的常数)
为大于0的常数)
(1)求椭圆方程;
(2)设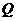 为椭圆上的一点,过点F、
为椭圆上的一点,过点F、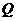 的直线
的直线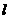 与
与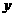 轴交于点M,若
轴交于点M,若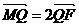 ,求
,求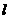 直线的斜率.
直线的斜率.
课后作业
班级_______学号__________姓名_________
3、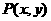 为椭圆
为椭圆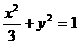 上的点,则点P到直线
上的点,则点P到直线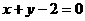 的最大距离为_________.
的最大距离为_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com