
题目列表(包括答案和解析)
22.本大题满分(14分)
 已知定点
已知定点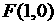 ,动点
,动点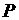 在
在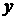 轴上运动,过点
轴上运动,过点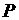 作
作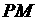 交
交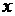 轴于点
轴于点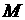 ,并延长
,并延长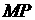 到点
到点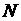 ,且
,且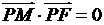 ,
,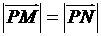 .
.
(1)求动点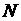 的轨迹方程;(2)直线
的轨迹方程;(2)直线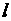 与动点
与动点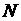 的轨迹交于
的轨迹交于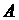 、
、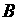 两点,若
两点,若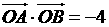 ,且
,且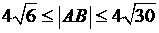 ,求直线
,求直线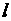 的斜率
的斜率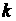 的取值范围.
的取值范围.
20.已知各项均为正数的数列{an}的前n项和为Sn,首项为a1,且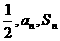 成等差数列。(1)求数列{an}的通项公式;(2)若
成等差数列。(1)求数列{an}的通项公式;(2)若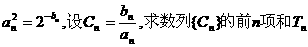
21 已知函数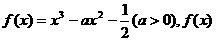 的导数的f′(x),若曲线y= f(x)上两点A、B处的切线都与x轴平行,且直线AB的斜率小于
的导数的f′(x),若曲线y= f(x)上两点A、B处的切线都与x轴平行,且直线AB的斜率小于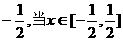 时,
时,
| f′(x)-3x2|≤2恒成立,求a的取值范围.
18. (12分)甲、乙、丙三个口袋内都分别装有6个不相同的球,并且每个口袋内的6个球均有1个红球,2个黑球,3个无色透明的球,现从甲、乙、丙三个口袋中依次随机各摸出1个球.求:(1)求恰好摸出红球、黑球和无色球各1个的概率;
(2)求摸出的3个球中含有有色球不少于2个的概率。
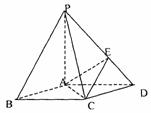 19.如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
19.如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=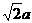 ,点E在PD上,且PE:ED=2:1(1)证明PA⊥平面ABCD
,点E在PD上,且PE:ED=2:1(1)证明PA⊥平面ABCD
(2)求以AC为棱, EAC与DAC为面的二面角θ的大小;
(3)在棱PC上是否存在一点F,使BE//平面AEC?证明你的结论。
17.(12分)已知向量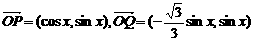 ,定义函数
,定义函数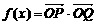 .
.
(1)求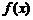 的最小正周期和最大值及相应的x值;(10分)
的最小正周期和最大值及相应的x值;(10分)
(2)当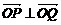 时,求x的值.(2分)
时,求x的值.(2分)
16、若两个向量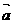 与
与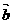 的夹角为q,则称向量“
的夹角为q,则称向量“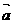 ×
×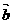 ”为“向量积”,其长度|
”为“向量积”,其长度|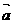 ×
×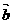 |=|
|=|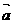 |•|
|•|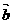 |•sinq。今已知|
|•sinq。今已知|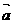 |=1,|
|=1,|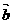 |=5,
|=5,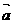 •
•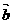 =-4,则|
=-4,则|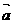 ×
×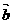 |= 。
|= 。
15.过椭圆的左焦点F且倾斜角为60°的直线交椭圆于A,B两点,若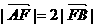 ,则椭圆的离心率e=
。
,则椭圆的离心率e=
。
14.若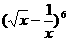 的展开式中的第五项是
的展开式中的第五项是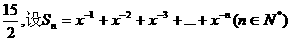 , Sn=
, Sn=
13.已知函数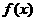 满足
满足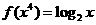 ,则
,则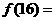
12.设 f (x)=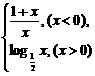 ,则f
(x)≥
,则f
(x)≥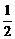 的解集是( )
的解集是( )
A.(-∞,-2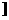 ∪
∪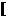
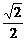 , +∞) B.
, +∞) B.
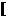 -2, 0)∪(0,
-2, 0)∪(0,
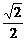
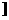
C. 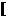 -2, 0)∪
-2, 0)∪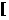
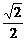 , +∞)
D. (-∞,-2
, +∞)
D. (-∞,-2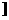 ∪(0,
∪(0, 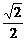
11.将棱长为3的正四面体以各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积为( )
A.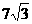 B.
B. 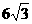 C
C 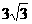 D.
D. 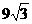
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com