
题目列表(包括答案和解析)
17.解:设每一局比赛甲获胜的概率为事件A,则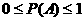
(1)由题意知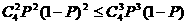 …………………………………………2分
…………………………………………2分
即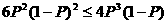 解得P=0或
解得P=0或 …………………………………4分
…………………………………4分
(2)甲获胜,则有比赛2局,甲全胜,或比赛3局,前2局甲胜1局,第3局甲胜,故
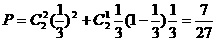 ……………………………………………………8分
……………………………………………………8分
(3)设“比赛6局,甲恰好胜3局”为事件C 则P(C)=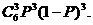 ………9分
………9分
当P=0或P=1时,显然有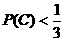 …………………………………………………10分
…………………………………………………10分
又当0<P<1时,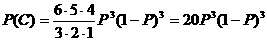
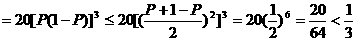 …………………………11分
…………………………11分
故甲恰好胜3局的概率不可能是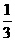 .……………………………………………………12分
.……………………………………………………12分
17.(本题满分12分) 甲,乙两人进行乒兵球比赛,在每一局比赛中,甲获胜的概率为P.
(1)如果甲,乙两人共比赛4局,甲恰好负2局的概率不大于其恰好胜3局的概率,试
求P的取值范围.
(2)若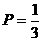 ,当采用3局2胜制的比赛规则时,求甲获胜的概率.
,当采用3局2胜制的比赛规则时,求甲获胜的概率.
(3)如果甲,乙两人比赛6局,那么甲恰好胜3局的概率可能是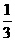 吗?为什么?
吗?为什么?
2、口袋里装有大小相同的4个红球和8个白球,甲、乙两人依规则从袋中有放回摸球,每次摸出一个球,规则如下:若一方摸出一个红球,则此人继续下一次摸球;若一方摸出一个白球,则由对方接替下一次摸球,且每次摸球彼此相互独立,并由甲进行第一次摸球.
(I)求在前三次摸球中,甲摸得红球的次数ξ的数学期望;
(II)设第n次由甲摸球的概率为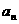 ,试建立
,试建立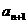 与
与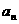 的递推关系,并求数列{
的递推关系,并求数列{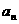 }的通项公式.
}的通项公式.
解:(I)记“甲摸球一次摸出红球”为事件A,“乙摸球一次摸出红球”为事件B,则
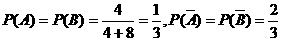 ,且A、B相互独立.………………(2分)
,且A、B相互独立.………………(2分)
据题意,ξ的可能取值为0,1,2,3,其中
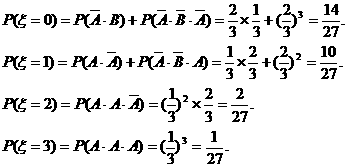
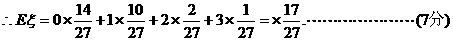
(II)据摸球规则可知,第n次由甲摸球包括如下两个事件:
①第n-1次由甲摸球,且摸出红球,其发生的概率为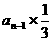 ;
;
②第n-1次由乙摸球,且摸出白球,其发生的概率为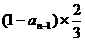 .
.
∵上述两个事件互斥,
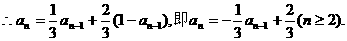 ……………………(10分)
……………………(10分)
由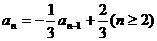
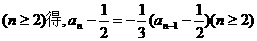 ,
,
∵甲进行第一次摸球,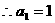 ,即
,即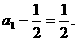 ………………………………(12分)
………………………………(12分)
∴数列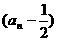 是首项为
是首项为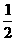 ,公比为-
,公比为-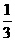 的等比数列,
的等比数列,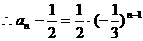 .
.
故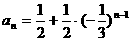 .……………………………………………………………(14分)
.……………………………………………………………(14分)
18、(1)质点向四个方向移动是一个必然事件,则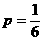 ;
;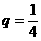 . (2)至少需要3秒才可以同时到达D,则当经过3秒,A到达D点的概率为
. (2)至少需要3秒才可以同时到达D,则当经过3秒,A到达D点的概率为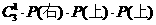
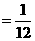 .设N
.设N ,C
,C ,H
,H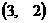 ,F
,F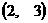 ,E
,E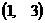 ,M
,M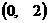 ,则经过3秒,B到时达D的可能情境共有9种. B到达D点的概率为
,则经过3秒,B到时达D的可能情境共有9种. B到达D点的概率为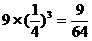 . 又B到达D点与A到达D点之间没有影响,则A,B同时到达的概率为
. 又B到达D点与A到达D点之间没有影响,则A,B同时到达的概率为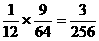
18、(本小题满分14分)平面上有两个质点A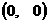 ,B
,B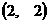 ,在某一时刻开始每隔1秒向上下左右任一方向移动一个单位. 已知质点A向左,右移动的概率都是
,在某一时刻开始每隔1秒向上下左右任一方向移动一个单位. 已知质点A向左,右移动的概率都是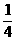 ,向上,下移动的概率分别是
,向上,下移动的概率分别是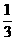 和
和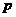 ,质点B向四个方向移动的概率均为
,质点B向四个方向移动的概率均为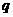 .(1)求
.(1)求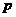 和
和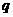 的值;(2)试判断至少需要几秒,A、B能同时到达D
的值;(2)试判断至少需要几秒,A、B能同时到达D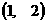 ,并求出在最短时间同时到达的概率?
,并求出在最短时间同时到达的概率?
18、(12分)2006年12月9日,在第十五届多哈亚运会羽毛球男子单打决赛中,排名世界第一的林丹迎战陶菲克,在此前一周内,林丹曾两次击败陶菲克,但在决赛中,林丹却意外地以0:2失利,与冠军擦肩而过,根据两人在以往的交战成绩分析,林丹在每一局的比赛中获胜的概率但是0.7,比赛按“三局二胜制”的规则进行(即先胜两局的选手获胜,比赛结束),且设各局之间互不影响;
⑴求林丹以0:2失利的概率;
⑵若林丹与陶菲克下次在比赛中再次相遇,请你计算林丹获胜的概率;
⑶若林丹与陶菲克下次在比赛中再次相遇,试求林丹的净胜局数的分布列和期望值。
17、(1)解:田忌获胜的概率是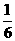 ;
;
(2)解:田忌获胜的概率是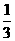 。
。
17.(本题满分12)田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A1、A2、A3;田忌的三匹马B1、B2、B3;三匹马各比赛一次,胜两场者为获胜,双方均不知对方的马出场顺序。
(1)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>A3>B3;则田忌获胜
的概率是多大?
(2)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>B3>A3;则田忌获胜
的概率是多大?
17、解:(1)当乙连胜四局时,对阵情况如下:
第一局:甲对乙,乙胜;第二局:乙对丙,乙胜;第三局:乙对甲,乙胜;第四局:乙对丙,乙胜.
所求概率为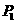 =
=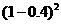 ×
×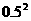 =
=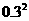 =0.09
=0.09
∴ 乙连胜四局的概率为0.09.-----------------------------------------------------6分
(2)丙连胜三局的对阵情况如下:
第一局:甲对乙,甲胜,或乙胜.
当甲胜时,第二局:甲对丙,丙胜.第三局:丙对乙,丙胜;第四局:丙对甲,丙胜.
当乙胜时,第二局:乙对丙,丙胜;第三局:丙对甲,丙胜;第四局:丙对乙,丙胜.
故丙三连胜的概率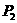 =0.4×
=0.4×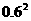 ×0.5+(1-0.4)×
×0.5+(1-0.4)×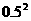 ×0.6=0.162.--------12分
×0.6=0.162.--------12分
17、(本小题满分12分)在一次由三人参加的围棋对抗赛中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,比赛按以下规则进行;第一局:甲对乙;第二局:第一局胜者对丙;第三局:第二局胜者对第一局败者;第四局:第三局胜者对第二局败者,求:
(1)乙连胜四局的概率;(2)丙连胜三局的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com