
题目列表(包括答案和解析)
1.已知函数: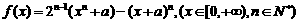
(Ⅰ)求函数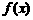 的最小值;
的最小值;
(Ⅱ)证明: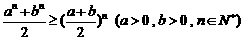 ;
;
(Ⅲ)定理:若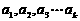 均为正数,则有
均为正数,则有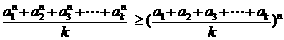 成立 (其中
成立 (其中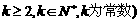 .请你构造一个函数
.请你构造一个函数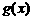 ,证明:当
,证明:当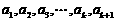 均为正数时,
均为正数时,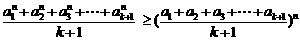 。
。
2.把一颗骰子投掷两次,第一次出现的点数记为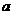 ,第二次出现的点数记为b,则方程组
,第二次出现的点数记为b,则方程组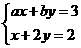 只有正数解(
只有正数解(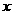 与
与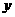 都为正)的概率为
。
都为正)的概率为
。
1.规定符号 “ * ”表示一种运算,即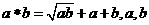 是正实数,已知
是正实数,已知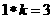 .则函数
.则函数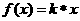 的取值范围是______.
的取值范围是______.
2.(理科)已知函数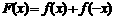 ,x∈R,且
,x∈R,且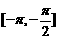 是函数
是函数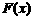 的单调递增区间,若将
的单调递增区间,若将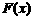 的图象按向量
的图象按向量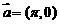 平移得到一个新函数
平移得到一个新函数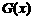 的图象,则函数
的图象,则函数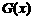 的单调递减区间必定是
的单调递减区间必定是
A.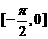 B.
B.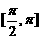 C.
C.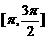 D.
D.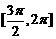
1.设函数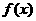 定义如下表,数列
定义如下表,数列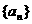 满足
满足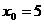 ,且对任意的自然数均有
,且对任意的自然数均有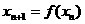 ,则
,则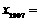
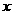 |
1 |
2 |
3 |
4 |
5 |
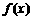 |
4 |
1 |
3 |
5 |
2 |
A.1 B.2 C.4 D.5
6.类比发现、归纳、推广的试题
数学创新思维是指对已掌握的数学知识和方法进行推广拓展,对未知数学领域通过探索得到新的结果的能力.高考中的这类命题,研究的立足点源于教材或双基,研究过程基于考生已有的知识结构,研究的目的是考查迁移能力,或更高层次的能力.
典型题12 (2003年上海高考题)已知数列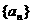 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和: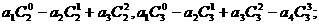
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
评注:本题主要考查探索能力、类比归纳能力和论证能力.
典型题13 (2004年上海市普通高校春季高考数学试卷)如图,点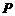 为斜三棱柱
为斜三棱柱
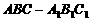 的侧棱
的侧棱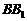 上一点,
上一点,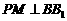 交
交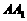 于点
于点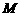 ,
,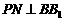 交
交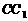 于点
于点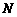 .
.
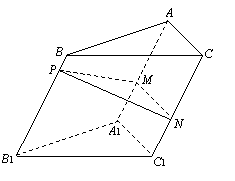 (1) 求证:
(1) 求证: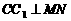 ;
;
(2) 在任意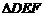 中有余弦定理:
中有余弦定理: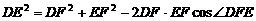 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
解 (1) 证:
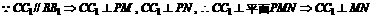 ;
;
(2) 解:在斜三棱柱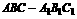 中,有
中,有
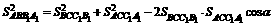 ,
,
其中 为平面
为平面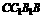 与平面
与平面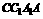 所组成的二面角. 证明略.
所组成的二面角. 证明略.
评注:本题考查学生的类比推广能力,作为能力立意的高考题,是一次很好的尝试.
典型题14 (2003年全国高考数学理科压卷试题)
(Ⅰ)设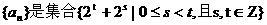 中所有的数从小到大排列成的数列,即
中所有的数从小到大排列成的数列,即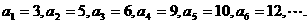 将数列
将数列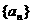 各项按照上小下大,左小右大的原则写成如下的三角形数表:
各项按照上小下大,左小右大的原则写成如下的三角形数表:
3
5 6
9 10 12
… … … …
… … … … …
……………
(i)写出这个三角形数表的第四行、第五行各数; (i i)求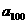 .
.
(Ⅱ)设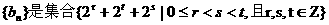 中所有的数都是从小到大排列成的数列,已知
中所有的数都是从小到大排列成的数列,已知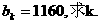
评注:本题以集合中元素排列的数表为背景,要求考生由表及里,层层深入地运用数学知识分析探索,揭示问题本质,具有较大的自由度和思维空间,渗透了研究性学习的理念.
从上面三例不难发现,此类试题不仅考查了考生的现有知识存量,更着重于考查未来知识增量,即发展潜能.
5.合作研究的试题
下面是国内的一个高考模拟试题,供参考:
典型题11 张老师给出一个函数y=f(x),请四名学生各指出其中一个性质:
学生甲:对于x∈R,都有f (x)= f (π-x);
学生乙:函数y= f (x)的图象关于原点对称;
学生丙:函数y= f (x)满足f (x +y)= f (x)·f (y)-f (2π-x)·f (2π-y);
学生丁:函数y= f (x)有最大值m和最小值n,且m≠n.
张老师说:你们四名同学中恰有3人说的是正确的,则张老师给出的函数可能是 .(只要写出一个适合的答案即可).
4.新定义题
类似地考查学习能力的题还很多,如新定义题:
典型题9 任取x1,
x2∈[a,b],且x1≠x2,若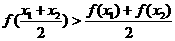 ,称f (x)是[a,b]上的凸函数,则下列图象中,是凸函数图象的是( ).
,称f (x)是[a,b]上的凸函数,则下列图象中,是凸函数图象的是( ).
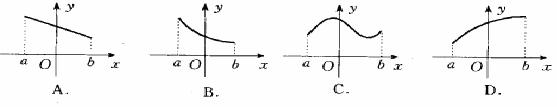
典型题10 (2004年北京市高考题)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.
已知数列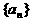 是等和数列,且
是等和数列,且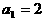 ,公和为5,那么
,公和为5,那么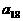 的值为______________,这个数列的前n项和
的值为______________,这个数列的前n项和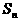 的计算公式为________________
的计算公式为________________
(答案3;当n为偶数时,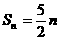 ;当n为奇数时,
;当n为奇数时,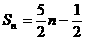 )
)
3.高观点试题
典型题8 (新编)设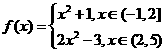
(1)对任意的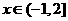 ,试比较
,试比较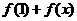 与
与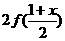 的大小.
的大小.
(2)对任意的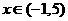 ,你在(1)中得到的结果是否仍然成立?请说明理由.
,你在(1)中得到的结果是否仍然成立?请说明理由.
评注:这是关于分段函数的凸性问题的试题,背景是凸函数的合成,考查分类讨论思想,综合能力.
2.学习成果展示题
典型题7:已知数列{an}的前n项和Sn=qn-1(q>0且q为常数),某同学研究此数列后,得出如下三个结论:
(1){an}的通项公式为an=(q-1)qn-1;
(2){an}是等比数列;
(3)当q≠1时,
其中结论正确的个数有 ( )
(A)0个 (B)1个 (C)2个 (D)3个
(答案:C)
评注:研究性课程作为新课程的必修课,成为高考内容是命题人积极倡导的,今后将会有更多的体现,研究性学习成果的评价是其中一个重要环节.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com