
题目列表(包括答案和解析)
5.在正方体A1B1C1D1-ABCD中,M、N分别是棱A1A和B1B的中点,若θ为直线CM与D1N所成的角,则sinθ等于 ( )
A. 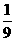 B.
B.
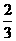 C.
C.
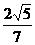 D.
D. 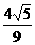
4.已知棱长都相等的正三棱锥内接于一个球,某人画出四个过球心的平面截球与正三棱锥所得的图形如下,则 ( ) A.以下四个图形都是正确的 B.只有(2)(4)是正确的 C.只有(4)是正确的 D.只有(1)(2)是正确的
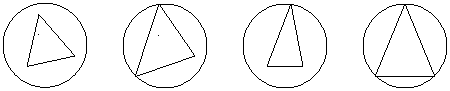
① ② ③ ④
3.已知正方体ABCD-A1B1C1D1的棱长为a,长为定值的线段EF在棱AB上移动(EF<a),若P是A1D1上的定点,Q是C1D1上的动点,则四面体PQEF的体积是 ( )
A.有最小值的一个变量 B.有最大值的一个变量
C.没有最值的一个变量 D.是一个常量
2.已知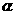 ∥
∥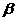 ,
,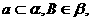 则在
则在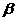 内过点
内过点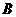 的所有直线中
( )
的所有直线中
( )
A.不一定存在与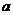 平行的直线
B.只有两条与
平行的直线
B.只有两条与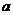 平行的直线
平行的直线
C.存在无数条与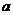 平行的直线
D.存在唯一一条与
平行的直线
D.存在唯一一条与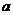 平行的直线
平行的直线
1.两两互相平行的直线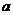 、
、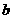 、
、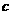 可以确定平面的个数是
( )
可以确定平面的个数是
( )
A.1或3 B.1 C.3 D.4
10.等比数列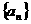 中,各项和
中,各项和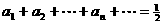 ,则
,则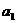 的取值范围是( )
的取值范围是( )
(A)(0。+∞) (B)(-∞,1)
(C)(0,1) (D)(0,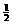 )∪(
)∪(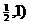
数列选择题专项训练答案
DCABA BCBAD
22.(本小题满分14分) 已知a>1,数列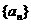 的通项公式是
的通项公式是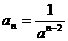 ,前n项和记作
,前n项和记作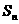 (n=1,2,…),规定
(n=1,2,…),规定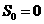 .函数
.函数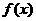 在
在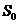 处和每个区间(
处和每个区间(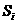 ,
,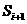 )(i=0,1,2,…)上有定义,且
)(i=0,1,2,…)上有定义,且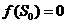 ,
,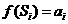 (i=1,2,…).当
(i=1,2,…).当 (
(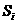 ,
,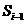 )时,f(x)的图像完全落在连结点
)时,f(x)的图像完全落在连结点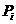 (
(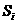 ,
,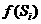 )与点
)与点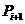 (
(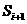 ,
,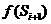 )的线段上.
)的线段上.
(Ⅰ)求f(x)的定义域;
(Ⅱ)设f(x)的图像与坐标轴及直线l: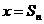 (n=1,2,…)围成的图形面积为
(n=1,2,…)围成的图形面积为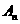 ,
,
求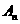 及
及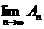 ;
;
(Ⅲ)若存在正整数n,使得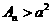 ,求a的取值范围.
,求a的取值范围.
21.(本小题满分12分)在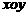 平面上有一系列点
平面上有一系列点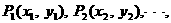
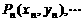 对每个自然数
对每个自然数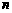 ,点
,点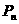 位于函数
位于函数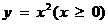 的图象上.以点
的图象上.以点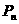 为圆心的⊙
为圆心的⊙ 与
与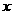 轴都相切,且⊙
轴都相切,且⊙ 与⊙
与⊙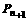 又彼此外切.若
又彼此外切.若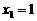 ,且
,且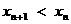
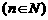 .
.
(Ⅰ)求证:数列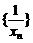 是等差数列;
是等差数列;
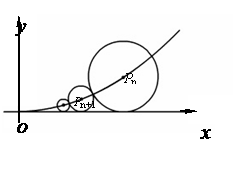 (Ⅱ)设⊙
(Ⅱ)设⊙ 的面积为
的面积为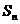 ,
,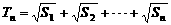 , 求证:
, 求证: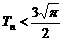
20.(本小题满分12分)如图所示,已知圆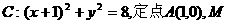 为圆上一动点,点P在AM上,点N在CM上,且满足
为圆上一动点,点P在AM上,点N在CM上,且满足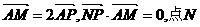 的轨迹为 曲线E.
的轨迹为 曲线E.
(I)求曲线E的方程;
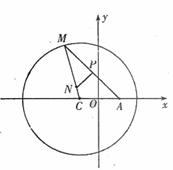 (II)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),
(II)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),
且满足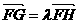 ,求
,求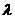 的取值范围.
的取值范围.
19.(本小题满分12分)为了能更好地了解鲸的生活习性,某动物研究所在受伤的鲸身上安装了电子监测装置,从海岸放归点A处(如图所示)把它放归大海,并沿海岸线由西到东不停地对鲸进行了40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动)。然后又在观测站B处对鲸进行生活习性的详细观测。已知AB=15km,观测站B的观测半径为5km.

|
观测时刻t(分钟) |
跟踪观测点到放归点距离a(km) |
鲸位于跟踪观测点正北方向的距离b(km) |
|
10 |
1 |
1 |
|
20 |
2 |
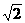 |
|
30 |
3 |
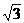 |
|
40 |
4 |
2 |
(I)根据表中数据:(1)计算鲸沿海岸线方向运动的速度,(2)写出a、b满足的关系式
并画出鲸的运动路线简图;
(II)若鲸继续以(I)-(2)中的运行路线运动,则鲸经过多少分钟(从放归时计时),
可进入前方观测站B的观测范围。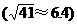
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com