
题目列表(包括答案和解析)
1、平面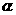 ⊥平面
⊥平面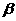 ,
,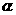 ∩
∩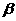 =
=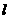 ,点P∈
,点P∈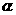 ,点Q∈
,点Q∈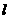 ,那么PQ⊥
,那么PQ⊥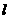 是PQ⊥
是PQ⊥ 的( )
的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
4、两个平面互相垂直,一条直线和其中一个平面平行,则这条直线与另一个平面的位置关系是 .
例题讲解
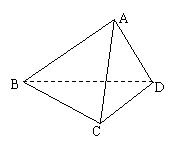 例1、在三棱锥A-BCD中,AB=3,AC=AD=2,且∠DAC=∠BAC=∠BAD=60°,
例1、在三棱锥A-BCD中,AB=3,AC=AD=2,且∠DAC=∠BAC=∠BAD=60°,
求证:平面BCD⊥平面ADC.
例2、如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1,CD的中点.
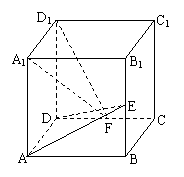 求证:平面AED⊥平面A1FD1.
求证:平面AED⊥平面A1FD1.
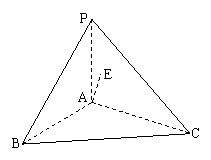
例3、如图,已知平面PAB⊥平面ABC,平面PAC⊥平面ABC,E是点A在平面PBC内的射影, (1)求证:PA⊥平面ABC; (2)当E为△PBC的垂心时,求证:△ABC是直角三角形.
课后作业
班级_______学号__________姓名_________
3、已知PA⊥正方形ABCD所在的平面,垂足为A,连结PB、PC、PD、AC、BD,则互相垂直的平面有__________对.
2、过平面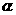 外两点且垂直平面
外两点且垂直平面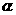 的平面
(
)
的平面
(
)
A.有且只有一个 B.有一个或两个
C.有且仅有两个 D.一个或无数个
1、已知直线m、n,平面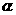 、
、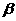 ,且m⊥
,且m⊥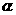 ,n
,n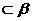 ,给出下列命题:①若
,给出下列命题:①若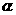 ∥
∥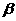 ,则
,则
m⊥n;②若m⊥n,则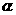 ∥
∥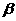 ;③若
;③若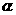 ⊥
⊥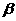 ,则m∥n;④若m∥n,则
,则m∥n;④若m∥n,则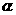 ⊥
⊥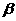 .其中正确的命题是
( )
.其中正确的命题是
( )
A.①④ B.①③ C.②③ D.③④
4、两平面垂直的性质定理.
重点难点
“线线垂直”、“线面垂直”、“面面垂直”的相互转化.
基础练习
3、两平面垂直的判定定理;
2、两平面垂直的定义;
1、二面角、二面角平面角的定义;
8、如图,斜三棱柱ABC-A1B1C1中,AB=BB1,BB1与底面成60°角,侧面A1B⊥底面ABC,△ABC是正三角形.
(1)证明:AB⊥B1C;
(2)证明:B1C⊥平面ABC1;
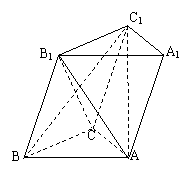 (3)求二面角B1-AC-B的大小.
(3)求二面角B1-AC-B的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com