
题目列表(包括答案和解析)
18.解:设梯形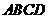 的面积为
的面积为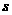 ,点P的坐标为
,点P的坐标为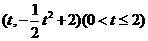 。
。
由题意得,点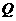 的坐标为
的坐标为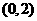 ,直线
,直线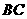 的方程为
的方程为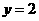 。
。
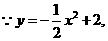
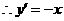
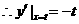 ………………………………………………………………3分
………………………………………………………………3分
 直线
直线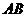 的方程为
的方程为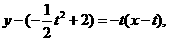
即: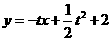 ………………………………………………5分
………………………………………………5分
令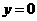 得,
得,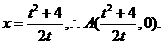
令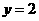 得,
得,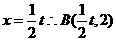
∴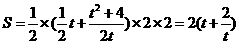 ……………………………8分
……………………………8分
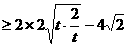 ………………………10分
………………………10分
当且仅当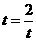 ,即
,即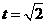 时,取“=”且
时,取“=”且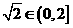 ,
,
∴当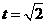 时,
时,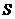 有最小值为
有最小值为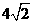 .
.
∴梯形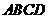 的面积的最小值为
的面积的最小值为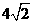 ……………………………………12分
……………………………………12分
17.(Ⅰ)解法一:
 成等差数列,
成等差数列,
∴  …………………………………………2分
…………………………………………2分
由正弦定理得,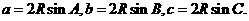
代入得,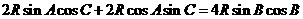
即:sin(A+C)=2sinBcosB
∵A+B+C=π
∴sin(A+C)=sinB
∴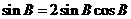 ……………………………………………………4分
……………………………………………………4分
又在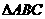 中,
中,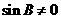 ,
,
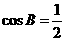

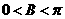 , ∴
, ∴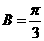 .……………………………………………………6分
.……………………………………………………6分
解法二:∵ 成等差数列,
成等差数列,
∴ …………………………………………2分
…………………………………………2分
由余弦定理,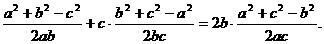
化简得, 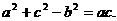 ……………………4分
……………………4分
∴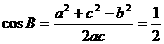
∵ 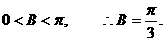 ……………………………………6分
……………………………………6分
(Ⅱ)解:
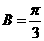 ,
,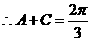
∴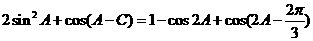 …………………8分
…………………8分
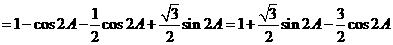
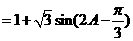 ……………………………………………………10分
……………………………………………………10分

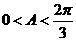 ,
,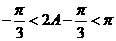
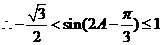 ……………………………………………13分
……………………………………………13分
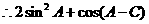 的范围是
的范围是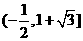 ……………………14分
……………………14分
|
等腰梯形ABCD的三边AB,BC,CD分别与函数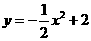 ,
,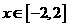 的图象切于点P,Q,R。.求梯形ABCD面积的最小值。
的图象切于点P,Q,R。.求梯形ABCD面积的最小值。

17.(本小题满分14分,第一小问满分6分,第二小问满分8分)
在△ABC中,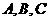 的对边分别为
的对边分别为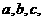 且
且 成等差数列.
成等差数列.
(Ⅰ)求B的值;
(Ⅱ)求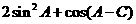 的范围。
的范围。
16.已知定义域为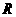 的函数
的函数 对任意实数
对任意实数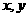 满足
满足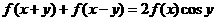 ,且
,且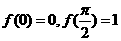 ,给出下列结论:
,给出下列结论:
①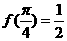 ;②
;② 为奇函数;③
为奇函数;③ 是周期函数;④
是周期函数;④ 在
在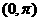 内为单调函数
内为单调函数
其中正确的结论是 ②③ (填上所有正确结论的序号)
14.已知某人投蓝的命中率为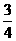 ,则此人投蓝4次,至少命中3次的概率是
,则此人投蓝4次,至少命中3次的概率是 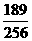 。
。
|
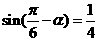 ,则
,则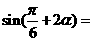
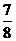 。
。13.已知函数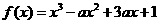 在区间
在区间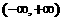 内既有极大值,又有极小值,则实数
内既有极大值,又有极小值,则实数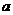 的取值范围是
的取值范围是
 。
。
12.在△ABC中,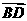
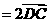 ,
,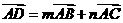 ,则
,则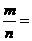
 。
。
11.为了考察甲、乙两种小麦的长势,分别从中抽取了6株苗,测得高如下(单位:cm):
|
甲 |
11 |
12 |
12 |
10 |
13 |
14 |
|
乙 |
12 |
13 |
9 |
13 |
12 |
13 |
由此可以估计, 甲 种小麦长得比较整齐。
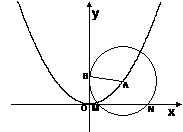
22.(本小题满分16分)
如图,已知圆 过定点
过定点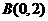 ,圆心
,圆心 在抛物线
在抛物线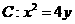 上运动,
上运动,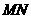 为圆
为圆 在
在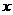 轴上所截得的弦.
轴上所截得的弦.
 (Ⅰ)证明:当
(Ⅰ)证明:当 点运动时,
点运动时,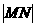 为定值.
为定值.
(Ⅱ)当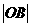 是
是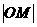 与
与 的等差中项时,
的等差中项时,
试判断抛物线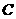 的准线与圆
的准线与圆 的位置关系,并说明理由.
的位置关系,并说明理由.
21.(本小题满分14分)
已知数列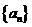 的前
的前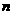 项和为
项和为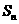 ,若
,若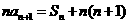 ,且
,且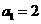 .
.
(Ⅰ)求数列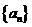 的通项公式;
的通项公式;
(Ⅱ)令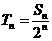 ,若对一切正整数
,若对一切正整数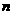 ,总有
,总有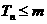 ,求
,求 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com